
math notes for class 12 download pdf continuity and differentiability chapter 5 , continuity and differentiability 12 notes, class 12 maths notes, continuity and differentiability class 12, continuity and differentiability class 12 notes, class 12 continuity and differentiability, note maths, maths notes, continuity and differentiability, class 12 cmaths chapter 5 notes, 12th standard maths notes, 12th std maths notes, class 12 maths notes chapter 5, continuity and differentiability chapter class 12 notes
The rate of change of a quantity y with respect to another quantity x is called the derivative or differential coefficient of y with respect to x .
Let f(x) is a function differentiable in an interval [a, b]. That is, at every point of the interval,
the derivative of the function exists finitely and is unique. Hence, we may define a new
function g: [a, b] → R, such that, ∀ x ∈ [a, b], g(x) = f’(x).
This new function is said to be differentiation (differential coefficient) of the function f(x) with respect to x and it is denoted by df(x) / d(x) or Df(x) or f’(x).
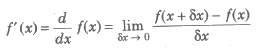
Let f(x) is a function finitely differentiable at every point on the real number line. Then, its derivative is given by
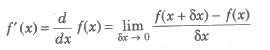
1. d / d(x) (xn) = nxn – 1, x ∈ R, n ∈ R
2. d / d(x) (k) = 0, where k is constant.
3. d / d(x) (ex) = ex
4. d / d(x) (ax) = ax loge a > 0, a ≠ 1


(v) if d / d(x) f(x) = φ(x), then d / d(x) f(ax + b) = a φ(ax + b)
(vi) Differentiation of a constant function is zero i.e., d / d(x) (c) = 0.
Geometrically derivative of a function at a point x = c is the slope of the tangent to the curve y
= f(x) at the point {c, f(c)}.
Slope of tangent at P = lim x → c f(x) – f(c) / x – c = {df(x) / d(x)} x = c or f’ (c).
If f and g are differentiable functions in their domain, then fog is also differentiable and
(fog)’ (x) = f’ {g(x)} g’ (x)
More easily, if y = f(u) and u = g(x), then dy / dx = dy / du * du / dx.
If y is a function of u, u is a function of v and v is a function of x. Then,
dy / dx = dy / du * du / dv * dv / dx.
In order to find differential coefficients of complicated expression involving inverse trigonometric functions some substitutions are very helpful, which are listed below .

If f(x, y) = 0, differentiate with respect to x and collect the terms containing dy / dx at one side
and find dy / dx.
Shortcut for Implicit Functions For Implicit function, put d /dx {f(x, y)} = – ∂f / ∂x / ∂f / ∂y,
where ∂f / ∂x is a partial differential of given function with respect to x and ∂f / ∂y means
Partial differential of given function with respect to y.
If x = f(t), y = g(t), where t is parameter, then dy / dx = (dy / dt) / (dx / dt) = d / dt g(t) / d / dt f(t) = g’ (t) / f’ (t)
Sometimes the given function can be deducted with the help of inverse Trigonometrical substitution and then to find the differential coefficient is very easy.

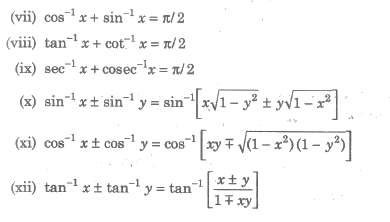
(i) If a function is the product and quotient of functions such as y = f1(x) f2(x) f3(x)… / g1(x)
g2(x) g3(x)… , we first take algorithm and then differentiate.
(ii) If a function is in the form of exponent of a function over another function such as
[f(x)]g(x) , we first take logarithm and then differentiate.
Let y = f(x) and z = g(x), then the differentiation of y with respect to z is dy / dz = dy / dx / dz / dx = f’ (x) / g’ (x)
If the function y = f(x) be differentiated with respect to x, then the result dy / dx or f’ (x), so obtained is a function of x (may be a constant).
Hence, dy / dx can again be differentiated with respect of x.
The differential coefficient of dy / dx with respect to x is written as d /dx (dy / dx) = d2y / dx2 or f’ (x). Again, the differential coefficient of d2y / dx2 with respect to x is written as d / dx (d2y / dx2) = d3y / dx3 or f”’(x)……
Here, dy / dx, d2y / dx2, d3y / dx3,… are respectively known as first, second, third, … order differential coefficients of y with respect to x. These alternatively denoted by f’ (x), f” (x), f”’
(x), … or y1, y2, y3…., respectively.
Note dy / dx = (dy / dθ) / (dx / dθ) but d2y / dx2 ≠ (d2y / dθ2) / (d2x / dθ2)
If u and v are functions of x such that their nth derivative exist, then
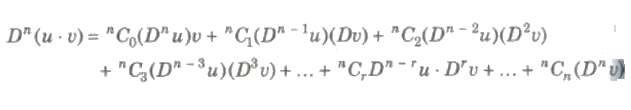

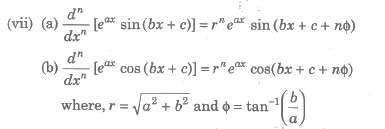

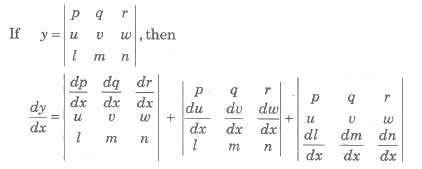
If g1 (x) and g2 (x) are defined in [a, b], Differentiable at x ∈ [a, b] and f(t) is continuous for g1(a) ≤ f(t) ≤ g2(b), then
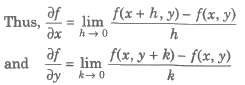
The partial differential coefficient of f(x, y) with respect to x is the ordinary differential coefficient of f(x, y) when y is regarded as a constant. It is a written as ∂f / ∂x or Dxf or fx.
![]()
e.g., If z = f(x, y) = x4 + y4 + 3xy2 + x4y + x + 2y
Then, ∂z / ∂x or ∂f / ∂x or fx = 4x3 + 3y2 + 2xy + 1 (here, y is consider as constant) ∂z / ∂y or ∂f / ∂y or fy = 4y3 + 6xy + x2 + 2 (here, x is consider as constant)
Let f(x, y) be a function of two variables such that ∂f / ∂x , ∂f / ∂y both exist.
(i) The partial derivative of ∂f / ∂y w.r.t. ‘x’ is denoted by ∂2f / ∂x2 / or fxx.
(ii) The partial derivative of ∂f / ∂y w.r.t. ‘y’ is denoted by ∂2f / ∂y2 / or fyy.
(iii) The partial derivative of ∂f / ∂x w.r.t. ‘y’ is denoted by ∂2f / ∂y ∂x / or fxy.
(iv) The partial derivative of ∂f / ∂x w.r.t. ‘x’ is denoted by ∂2f / ∂y ∂x / or fyx.
Note ∂2f / ∂x ∂y = ∂2f / ∂y ∂x
These four are second order partial derivatives.
If f(x, y) be a homogeneous function in x, y of degree n, then x (&partf / ∂x) + y (&partf / ∂y) = nf
If f(x, y) is a homogeneous function in x, y of degree n, then
(i) x (∂2f / ∂x2) + y (∂2f / ∂x ∂y) = (n – 1) &partf / ∂x
(ii) x (∂2f / ∂y ∂x) + y (∂2f / ∂y2) = (n – 1) &partf / ∂y
(iii) x2 (∂2f / ∂x2) + 2xy (∂2f / ∂x ∂y) + y2 (∂2f / ∂y2) = n(n – 1) f(x, y)
If α is m times repeated root of the equation f(x) = 0, then f(x) can be written as f(x) =(x – α)m g(x), where g(α) ≠ 0.
From the above equation, we can see that f(α) = 0, f’ (α) = 0, f” (α) = 0, … , f(m – l) ,(α) = 0.
Hence, we have the following proposition f(α) = 0, f’ (α) = 0, f” (α) = 0, … , f(m – l) ,(α) = 0.
Therefore, α is m times repeated root of the equation f(x) = 0.
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.