
ncert math notes for class 12 integrals download in pdf chapter 7 , integral 12 notes, class 12 maths notes, integral class 12, integral class 12 notes, class 12 integral, note maths, maths notes, integral, class 12 cmaths chapter 7 notes, 12th standard maths notes, 12th std maths notes, class 12 maths notes chapter 7, integral chapter class 12 notes
Let f(x) be a function. Then, the collection of all its primitives is called the indefinite integral of f(x) and is denoted by ∫f(x)dx. Integration as inverse operation of differentiation. If d/dx {φ(x)) = f(x), ∫f(x)dx = φ(x) + C, where C is called the constant of integration or arbitrary
Symbols f(x) → Integrand
f(x)dx → Element of integration
∫→ Sign of integral
φ(x) → Anti-derivative or primitive or integral of function f(x)
The process of finding functions whose derivative is given, is called anti-differentiation or
integration.

If d/dx {φ(x)} = f (x), then ∫f(x)dx = φ(x) + C. For different values of C, we get different functions, differing only by a constant. The graphs of these functions give us an infinite family of curves such that at the points on these curves with the same x-coordinate, the tangents are parallel as they have the same slope φ’(x) = f(x).
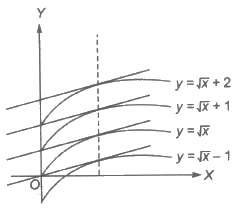
Consider the integral of 1/2√x
i.e., ∫1/2√xdx = √x + C, C ∈ R
Above figure shows some members of the family of curves given by y = + C for different C ∈ R.
(i) Both differentiation and integration are linear operator on functions as
d/dx {af(x) ± bg(x)} = a d/dx{f(x) ± d/dx{g(x)} and ∫[a.f(x) ± b.g(x)dx = a ∫f(x)dx ± b ∫g(x)dx
(ii) All functions are not differentiable, similarly there are some function which are not
integrable.
(iii) Integral of a function is always discussed in an interval but derivative of a function can be
(iv) Geometrically derivative of a function represents slope of the tangent to the graph of
function at the point. On the other hand, integral of a function represents an infinite family of
curves placed parallel to each other having parallel tangents at points of intersection of the
curves with a line parallel to Y-axis.
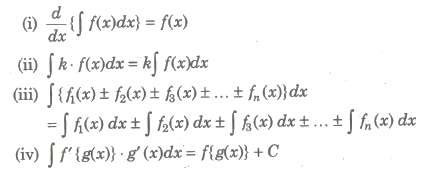
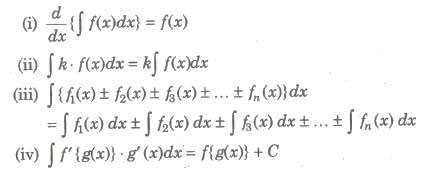
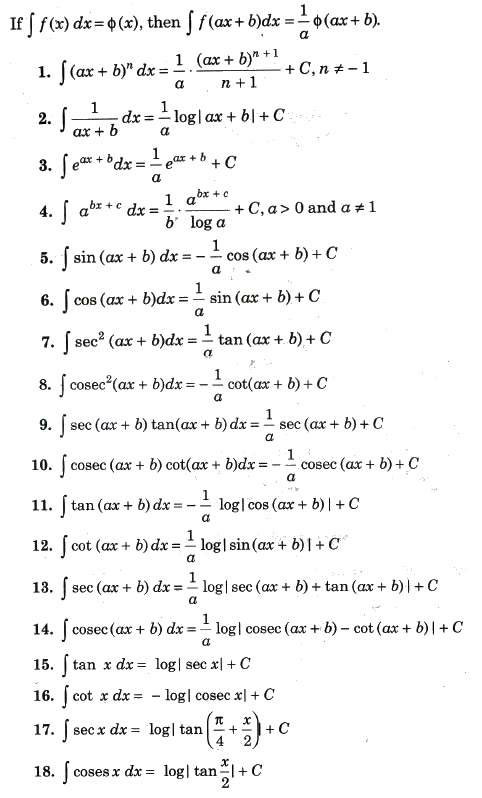
If degree of the numerator of the integrand is equal to or greater than that of denominator
divide the numerator by the denominator until the degree of the remainder is less than that of
denominator i.e.,
(Numerator / Denominator) = Quotient + (Remainder / Denominator)


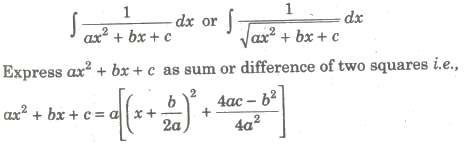
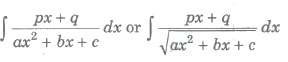
Put px + q = λd / dx (ax2 + bx + c) + mu; Now, find values of λ and mu; and integrate.
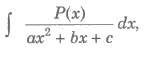
when P(x) is a polynomial of degree 2 or more carry out the dimension and express in the form P(x) / (ax2 + bx + c) = Q(x) + R(x) / (ax2 + bx + c), where R(x) is a linear expression or constant, then integral reduces to the form discussed earlier.
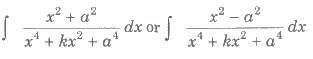
After dividing both numerator and denominator by x2, put x – a2 / x = t or x + (a2 / x) = t.
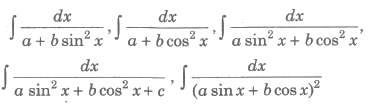
To evaluate the above type of integrals, we proceed as follow (a) Divide numerator and denominator by cos2x. (b) Rreplace sec2x, if any in denominator by 1 + tan2 x. (c) Put tan x = t, then sec2xdx = dt
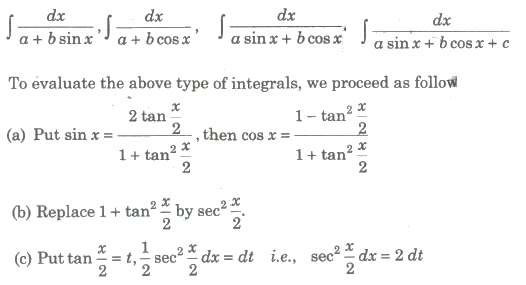


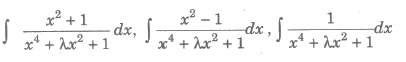
To evaluate the above type of integrals, we proceed as follows
• Divide numerator and denominator by x2
• Express the denominator of integrands in the form of (x + 1/x)2 ± k2
• Introduce (x + 1/x) or d (x – 1/x) or both in numerator.
• Put x + 1/x = t or x – 1/x = t as the case may be.
• Integral reduced to the form of ∫ 1 / x2 + a2dx or ∫ 1 / x2 + a2dx
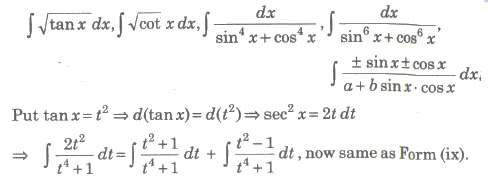
This method is used to integrate the product of two functions. If f(x) and g(x) be two integrable functions, then
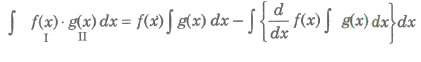
(i) We use the following preferential order for taking the first function. Inverse→ Logarithm→ Algebraic → Trigonometric→ Exponential. In short we write it HATE.
(ii) If one of the function is not directly integrable, then we take it a the first function.
(iii) If only one function is there, i.e., ∫log x dx, then 1 (unity) is taken as second function.
(iv) If both the functions are directly integrable, then the first function is chosen in such a way that its derivative vanishes easily or the function obtained in integral sign is easilY integrable.
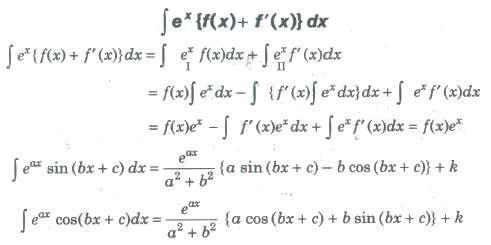
(i) If f(x) and g(x) are two polynomials, then f(x) / g(x) defines a rational algebraic function of
x. If degree of f(x) < degree of g(x), then f(x) / g(x) is called a proper rational function.
(ii) If degree of f(x) ≥ degree of g(x), then f(x) /g(x) is called an improper g(x) rational
function.
(iii) If f(x) / g(x) isan improper rational function, then we divide f(x) by g(x) g(x) and convert it into a proper rational function as f(x) / g(x) = φ(x) + h(x) / g(x).
(iv) Any proper rational function f(x) / g(x) can be expressed as the sum of rational functions
each having a simple factor of g(x). Each such fraction is called a partial fraction and the
process of obtaining them, is called the resolution or decomposition of f(x) /g(x) partial
fraction.

Case I. When g(x) is expressible as the product of non-repeated line factors.
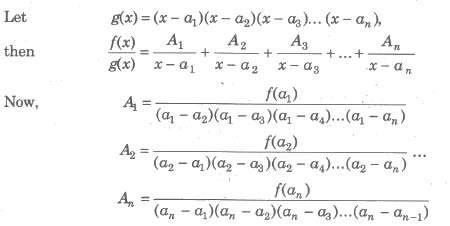
Trick To find Ap put x = a in numerator and denominator after P deleting the factor (x — ap).
Case II. When g(x) is expressible as product of repeated linear factors.
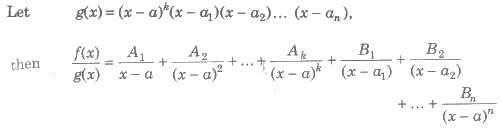
Here, all the constant cannot be calculated by using the method in Case I. However, Bl, B2, B3, … , Bn can be found using the same method i.e., shortcut can be applied only in the case of non-repeated linear factor.
Irrational function of the form of (ax + b)1/n and x can be evaluated by substitution (ax + b) = tn, thus

Integrals of the Type (bxm + bxn)P
Case I. If P ∈ N (natural number) we expand the binomial theorem and integrate.
Case II. If P ∈ Z (integers), put x = pk, where k denominator of m and n.
Case III. If (m+1)/n is an integer, we put (a + bxn) = rk, where k is th denominator of the fraction.
• ∫sinh x dx = cosh x + C
• ∫cosh x dx = sinh x + C
• ∫sech2x dx = tanh x + C
• ∫cosech2x dx = – coth x + C
• ∫sech x tanh x dx = – sech x + C
• ∫cosech x coth x dx = – cosech x + C
Case IV If {(m+1)/n} + P is an integer, we put (a + bxn) = rkxn is the denominator of the fraction p.

Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.