Inverse Trigonometric Functions Class 12 Notes For Maths Chapter 2

NCERT Notes Mathematics for Class 12

Chapter 2: Inverse Trigonometric Functions

Function

If y = f(x) and x = g(y) are two functions such that f (g(y)) = y and g (f(y)) = x, then f and y are said to be inverse of each other
i.e., g = f^-1 IF y = f(x), then x = f^-1(y)

Inverse Trigonometric Functions

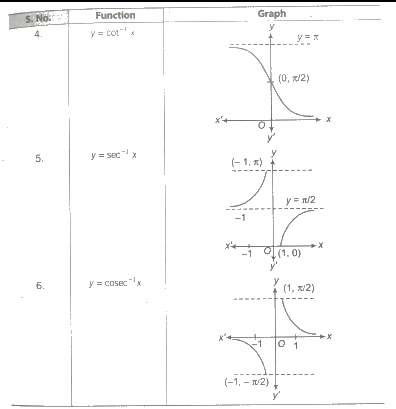
If y = sin X^-1, then x = sin^-1 y, similarly for other trigonometric functions.
This is called inverse trigonometric function .
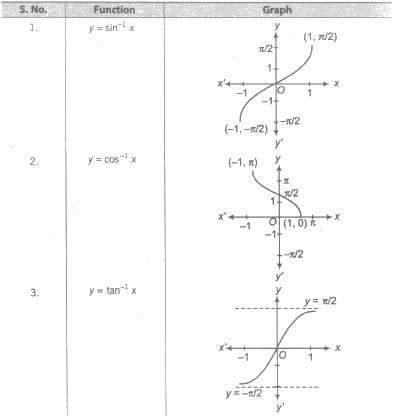
Now, y = sin^-1(x), y ∈ [π / 2 , π / 2] and x ∈ [-1,1].
(i) Thus, sin^-1x has infinitely many values for given x ∈ [-1, 1].
(ii) There is only one value among these values which lies in the interval [π / 2 , π / 2]. This value is called the principal value.

Domain and Range of Inverse Trigonometric FunctionsGraphs of Inverse Trigonometric
Functions

Properties of Inverse Trigonometric Functions

Property I

Property II

Property III

Property IV

Property V

Property VI

Property VII

Property VIII

Property IX

Property X

Property XI

Property XII

Important Results

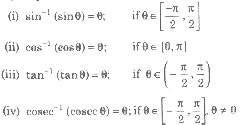
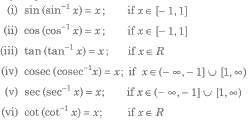
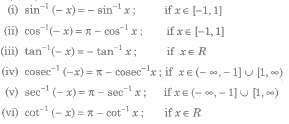
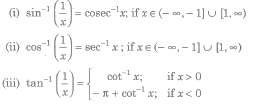
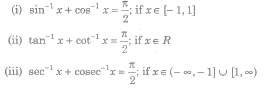
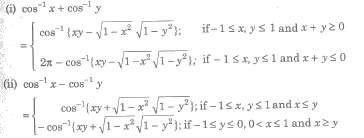
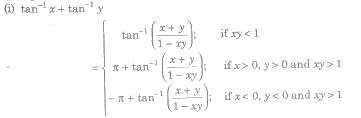
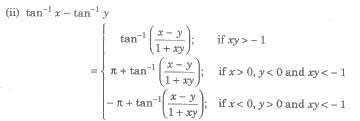
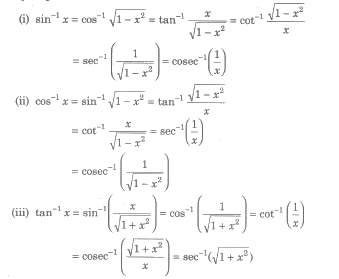
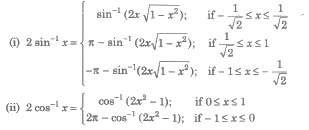
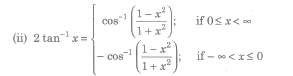
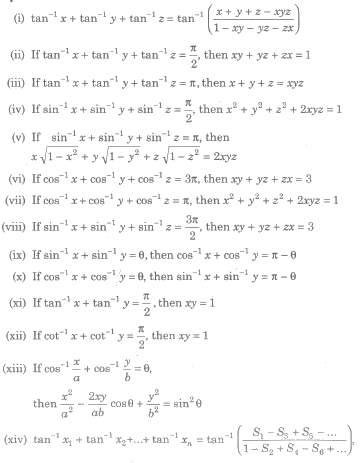
where S_k denotes the sum of the product of x₁,x₂,…x_n takes k at a time.

Inverse

Trigonometric Equation

An equation involving one or more trigonometrical ratios of unknown angle is called a trigonometric equation .

Solution/Roots of a Trigonometric Equation

A value of the unknown angle which satisfies the given equation, is called a solution or root of the equation.
The trigonometric equation may have infinite number of solutions.
(i) Principal Solution – The least value of unknown angle which satisfies the given equation, is called a principal solution of trigonometric equation.
(ii) General Solution – We know that, trigonometric function are periodic and solution of trigonometric equations can be generalised with the help of the periodicity of the trigonometric functions.
The solution consisting of all possible solutions of a trigonometric equation is called its general solution.

Important Results

Important Points to be Remembered

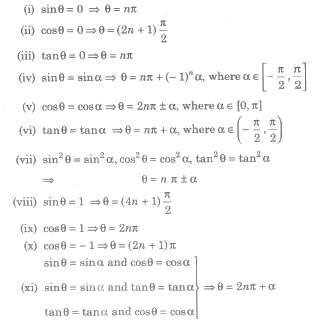
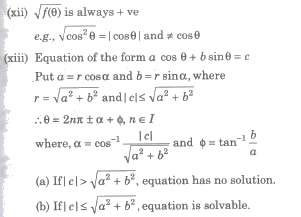
(i) While solving an equation, we have to square it, sometimes the resulting roots does not satisfy the original equation.
(ii) Do not cancel common factors involving the unknown angle on LHS and RHS.Because it may be the solution of given equation.
(iii) (a) Equation involving sec θ or tan θ can never be a solution of the form (2n + 1) π / 2.
(b) Equation involving coseca or cote can never be a solution of the form θ = nπ.

Ncert Solution for class 6 to 12 download in pdf