
math notes for class 12 linear programming chapter 12 download pdf, linear programming 12 notes, class 12 maths notes, linear programming class 12, linear programming class 12 notes, class 12 linear programming, note maths, maths notes, linear programming, class 12 cmaths chapter 12 notes, 12th standard maths notes, 12th std maths notes, class 12 maths notes chapter 12, linear programming chapter class 12 notes
It is an important optimization (maximization or minimization) technique used in decision making is business and everyday life for obtaining the maximum or minimum values as required of a linear expression to satisfying certain number of given linear restrictions.
The linear programming problem in general calls for optimizing a linear function of variables called the objective function subject to a set of linear equations and/or linear inequations called the constraints or restrictions.
The function which is to be optimized (maximized/minimized) is called an objective function.
The system of linear inequations (or equations) under which the objective function is to be optimized is called constraints.
All the variables considered for making decisions assume non-negative values.
A general LPP can be stated as (Max/Min) z = clxl + c2x2 + … + cnxn (Objective function) subject to constraints
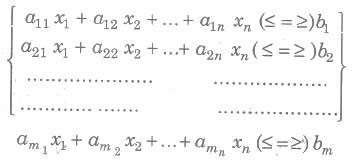
and the non-negative restrictions xl, x2,….., xn ≥ 0 where all al1, al2,…., amn; bl, b2,…., bm; cl, c2,…., cn are constants and xl, x2,…., xn are variables.
The positive variables which are added to left hand sides of the constraints to convert them into equalities are called the slack variables. The positive variables which are subtracted from the left hand sides of the constraints to convert them into equalities are called the surplus variables.
(i) Solution of a LPP A set of values of the variables xl, x2,…., xn satisfying the constraints of
a LPP is called a solution of the LPP.
(ii) Feasible Solution of a LPP A set of values of the variables xl, x2,…., xn satisfying the constraints and non-negative restrictions of a LPP is called a feasible solution of the LPP.
(iii) Optimal Solution of a LPP A feasible solution of a LPP is said to, be optimal (or optimum), if it also optimizes the objective function of the
problem.
(iv) Graphical Solution of a LPP The solution of a LPP obtained by graphical method i.e., by
drawing the graphs corresponding to the constraints and the non-negative restrictions is called the graphical solution of a LPP.
(v) Unbounded Solution If the value of the objective function can be increased or decreased
indefinitely, such solutions are called unbounded solutions.
(vi) Fundamental Extreme Point Theorem An optimum solution of a LPP, if it exists, occurs at one of the extreme points (i.e., corner points) of the convex
Polygon of the set of all feasible solutions.
The graph or the solution set of a system of simultaneous linear inequations is the region containing the points (x, y) which satisfy all the inequations of the given system
simultaneously.
To draw the graph of the simultaneous linear inequations, we find the region of the xy-plane, common to all the portions comprWng the solution sets of the given inequations. If there is no region common to all the solutions of the given inequations, we say that the solution set of the system of inequations is empty.
Note The solution set of simultaneous linear inequations may be an empty set or it may be the region bounded by the straight lines corresponding to given linear inequations or it may be an unbounded region with straight line boundaries.
There are two techniques of solving a LPP by graphical method
1. Corner point method and
2. Iso-profit or Iso-cost method
1. Corner Point Method
This method of solving a LPP graphically is based on the principle of extreme point theorem.
(i) Consider each constraint as an equation.
(ii) Plot each equation on graph, as each one will geometrically represent a straight line.
(iii) The common region, thus obtained satisfying all the constraints and the non-negative restrictions is called the feasible region. It is a convex polygon.
(iv) Determine the vertices (corner points) of the convex polygon. These vertices are known as
the extreme points of corners of the feasible region.
(v) Find the values of the objective function at each of the extreme points. The point at which the value of the objective function is optimum (maximum or minimum) is the optimal solution of the given LPP.
(i) Consider each constraint as an equation.
(ii) Plot each equation on graph as each one will geometrically represent a straight line.
(iii) The polygonal region so obtained, satisfying all the constraints and the non-negative
restrictions is the convex set of all feasible solutions of the given LPP, which is also known as
feasible region.
(iv) Determine the extreme points of the feasible region.
(v) Give some convenient value k to the objective function Z and draw the corresponding
straight line in the xy-plane.
(vi) If the problem is of maximization, then draw lines parallel to the line Z = k and obtain a
line which is farthest from the origin and has atleast one point common to the feasible region.
If the problem is of minimization, then draw lines parallel to the line Z = k and obtain a line,
which is nearest to the origin and has atleast one point common to the feasible region.
(vii) The common point so obtained is the optimal solution of the given LPP.
Consider the constraint ax + by ≤ c, where c > 0.
First draw the straight line ax + by = c by joining any two points on it. For this find two convenient points satisfying this equation.This straight line divides the xy-plane in two parts. The inequation ax + by c will represent that part of the xy-plane which lies to that side of the line ax + by = c in which the origin lies.
Again, consider the constraint ax + by ≥ c, where c > 0.
Draw the straight line ax + by = c by joining any two points on it.
This straight line divides the xy-plane in two parts. The inequation ax + by ≥ c will represent that part of the xy-plane, which lies to that side of the line ax + by = c in which the origin does not lie.
A BFS is a basic solution which also satisfies the non-negativity restrictions.
A BFS is said to be optimum, if it also optimizes (Max or min) the objective function.
1. Point Sets Point sets are sets whose elements are points or vectors in En or Rn (ndimensional euclidean space).
2. Hypersphere A hypersphere in En with centre at ‘a’ and radius ∈ > 0 is defined to be the set of points X = -{x:|x — a| = ∈}
3. An ∈ neighbourhood An & neighbourhood about the point ‘a is defined as the set of points lying inside the hypersphere with centre at ‘a’ and radius ∈ > 0.
4. An Interior Point A point ‘a’ is an interior point of the set S, if there exists an ∈ neighbourhood about ‘a’ which contains only points of the set S.
5. Boundary Point A point ‘a’ is a boundary point of the set S if every ∈ neighbourhood about ‘a’ contains points which are in the set and the points which are not in the set.
6. An Open. Set A set S is said to be an open set, if it contain only the interior points.
7. A Closed Set A set S is said to be a closed set, if it contains a its boundary points.
8. Lines In En the line through the two points x1 and x2, x1 ≠ x2 is defined to be the set of points.
X = {x: x = λ x1 + (1 — λ) x2, for all real λ}
9. Line Segments In En, the line segment joining two point x1 and x2 is defined to be the set of points.
X = {x:x = λ x1 + (1 — λ)x2, 0 ≤ λ ≤ 1}
10. Hyperplane A hyperplane is defined as the set of points satisfying c1x1+ c2x2 + …+ cnxn = z (not all ci = 0) or cx = z for prescribed values of c1, c2,…, cn and z.
11. Open and Closed Half Spaces
A hyperplane divides the whole space En into three mutually disjoint sets given by
X1 = {x : cx >z}
X2 = {x : cx = z}
X3 = {x : cx < z}
The sets x1 and x2 are called ‘open half spaces’. The sets {x : cx ≤ z} and { x : cx ≥ z} are
called ‘closed half spaces’.
12. Parallel Hyperplanes Two hyperplanes c1x = z1 and c2x = z2 are said to be parallel, if they have the same unit normals i.e., if c1 = Xc2 for λ, λ being non-zero.
13. Convex Combination A convex combination of a finite number of points x1, x2,…., xn is defined as a point x = λ1 x1 + λ2x2 + …. + λnxn, where λi is real and ≥ 0, ∀ and
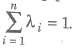
14. Convex Set A set of points is said to be convex, if for any two points in the set, the line segment joining these two points is also in the set.
or A set is convex, if the convex combination of any two points in the set, is also in the set.
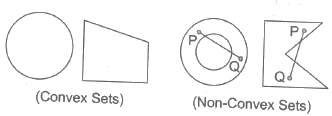
15 Extreme Point of a Convex Set A point x in a convex set c is called an ‘extreme point’, if x cannot be expressed as a convex combination of any two distinct points x1 and x2 in c.
16. Convex Hull The convex hull c(X) of any given set of points X is the set of all convex combinations of sets of points from X.
17. Convex Function A function f(x) is said to be strictly convex at x, if for any two other distinct points x1 and x2.
f{ λx1 + (1 — λ)x2} < λf(x1) + (1— λ)f(x2), where 0 < λ < 1.
And a function f(x) is strictly concave, if — f(x) is strictly convex.
18. Convex Polyhedron The set of all convex combinations of finite number of points is called the convex polyhedron generated by these points.
(i) A hyperplane is a convex set.
(ii) The closed half spaces H1 = {x : cx ≥ z} and H2 = {x : cx ≤ z} are convex sets.
(iii) The open half spaces : {x : cx > z} and {x : cx < z} are convex sets.
(iv) Intersection of two convex sets is also a convex sets.
(v) Intersection of any finite number of convex sets is also a convex set.
(vi) Arbitrary intersection of convex sets is also a convex set.
(vii) The set of all convex combinations of a finite number of points X1, X2,…., Xn is convex
set.
(viii) A set C is convex, if and only if every convex linear combination of points in C, also
belongs to C.
(ix) The set of all feasible solutions (if not empty) of a LPP is a convex set.
(x) Every basic feasible solution of the system Ax = b,x ≥ 0 is an extreme point of the convex
set of feasible solutions and conversely.
(xi) If the convex set of the feasible solutions of Ax = b,x ≥ 0 is a convex polyhedron, then
atleast one of the extreme points gives an optimal solution.
(xii) If the objective function of a LPP assumes its optimal value at more than one extreme
point, then every convex combination of these extreme points gives the optimal value of the
objective function.
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.