
math notes for class 12 download pdf application of derivatives chapter 6, application of derivatives 12 notes, class 12 maths notes, application of derivatives class 12, application of derivatives class 12 notes, class 12 application of derivatives, note maths, maths notes, application of derivatives, class 12 cmaths chapter 6 notes, 12th standard maths notes, 12th std maths notes, class 12 maths notes chapter 6, application of derivatives chapter class 12 notes
The derivative of the curve y = f(x) is f ‗(x) which represents the slope of tangent and equation of the tangent to the curve at P is
![]()
where (x, y) is an arbitrary point on the tangent.
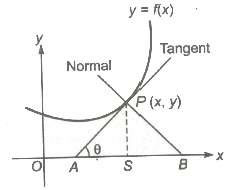
The equation of normal at (x, y) to the curve is
![]()
1. If![]() then the equations of the tangent and normal at (x, y) are (Y –
y) = 0 and (X – x) = 0, respectively.
then the equations of the tangent and normal at (x, y) are (Y –
y) = 0 and (X – x) = 0, respectively.
2. If![]() then the equation of the tangent and normal at (x, y) are (X – x)
= 0 and (Y – y) = 0, respectively.
then the equation of the tangent and normal at (x, y) are (X – x)
= 0 and (Y – y) = 0, respectively.
(i) If the tangent at P is perpendicular to x-axis or parallel to y-axis,
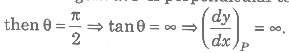
(ii) If the tangent at P is perpendicular to y-axis or parallel to x-axis,
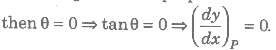
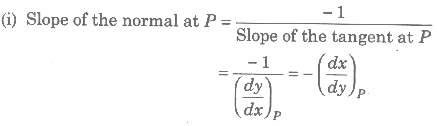
(ii) If![]() , then normal at (x, y) is parallel to y-axis and perpendicular to x-axis.
, then normal at (x, y) is parallel to y-axis and perpendicular to x-axis.
(iii) If![]() then normal at (x, y) is parallel to x-axis and perpendicular to y-axis.
then normal at (x, y) is parallel to x-axis and perpendicular to y-axis.
(i) Length of tangent, PA = y cosec θ =

(ii) Length of normal,
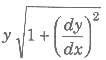
(iii) Length of subtangent,
![]()
(iv) Length of subnormal,
![]()
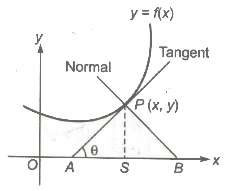
Let y = f1(x) and y = f2(x) be the two curves, meeting at some point P (x1, y1), then the angle between the two curves at P (x1, y1) = The angle between the tangents to the curves at P (x1, y1)
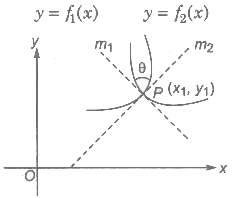
The other angle between the tangents is (180 — θ). Generally, the smaller of these two angles
is taken to be the angle of intersection.
∴ The angle of intersection of two curves θ is given by

If a variable quantity y is some function of time t i.e., y = f(t), then small change in Δt time At
have a corresponding change Δy in y.
Thus, the average rate of change = (Δy/Δt)
When limit At Δt→ 0 is applied, the rate of change becomes instantaneous and we get the rate
of change with respect to at the instant x.
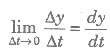
So, the differential coefficient of y with respect to x i.e., (dy/dx) is nothing but the rate of increase of y relative to x.
Let f be a real-valued function defined in the closed interval [a, b], such that
1. f is continuous in the closed interval [a, b].
2. f(x) is differentiable in the open interval (a, b).
3. f(a)= f(b)
Then, there is some point c in the open interval (a, b), such that f‘ (c) = 0.
Geometrically Under the assumptions of Rolle‘s theorem, the graph of f(x) starts at point (a, 0) and ends at point (b, 0) as shown in figures.
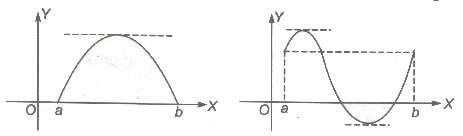
The conclusion is that there is at least one point c between a and b, such that the tangent to the graph at (c, f(c)) is parallel to the x-axis.
Between any two roots of a polynomial f(x), there is always a root of its derivative f‘ (x).
Let f be a real function, continuous on the closed interval [a, b] and differentiable in the open interval (a, b). Then, there is at least one point c in the open interval (a, b), such that
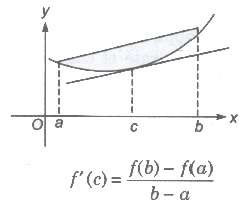
Geometrically Any chord of the curve y = f(x), there is a point on the graph, where the tangent
is parallel to this chord.
Remarks In the particular case, where f(a) = f(b).
The expression [f(b) – f(a)/(b – a)] becomes zero. Thus, when
f(a) = f (b), f ‗ (c) = 0 for some c in (a, b).
Thus, Rolle‘s theorem becomes a particular case of the mean value theorem.
1. Let y = f(x) be a given function. Let Ax denotes a small increment in Δx, corresponding which y increases by Δy. Then, for small increments, we assume that
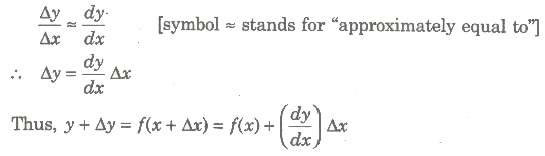
2. Let Δx be the error in the measurement of independent variable x and Δy is corresponding error in the measurement of dependent variable y. Then,
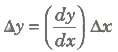
• Δy = Absolute error in measurement of y
• (Δy/y) = Relative error in measurement of y
• (Δy/y) * 100 = Percentage error in measurement of y
A function f(x) is said to be monotonic on an interval (a, b), if it is either increasing or decreasing on (a, b).
f(x) is said to be increasing in D1, if for every x1, x2 ∈ D1, x1 > x2 ⇒ f(x1) > f(x2). It means that there is a certain increase in the value of f(x) with an increase in the value of x.

f(x) is said to be non-decreasing in D1, if for every x1, x2 ∈ D1, x1 > x2 ⇒ f(x1) ≥ f(x2). It means that the value of f(x) would new decrease with an increase in the value of x.
f(x) is said to be decreasing in D1, if for every x1, x2 ∈ D1, x1 > x2 ⇒ f(x1) < f(x2). It means that there is a certain decrease in the value c f(x) with an increase in the value of x.
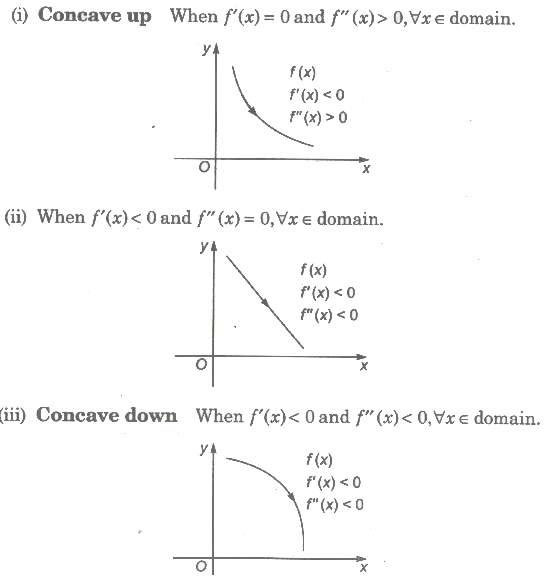
f(x) is said to be non-increasing in D1, if for every x1, x2 ∈ D1, x1 > x2 ⇒ f(x1) ≤ f(x2). It means
that the value of f(x) would never increase with an increase in the value of x.
If a function is either strictly increasing or strictly decreasing, then it is also a monotonic function.
(i) A function f (x) is said to be increasing (decreasing) at point x0, if there is an interval (x0 —
h, x0 + h) containing x0, such that f(x) is increasing (decreasing) on (x0 — h, x0 + h).
(ii) A function f (x) is said to be increasing on [a , b], if it is increasing (decreasing) on (a ,b)
and it is also increasing at x = a and x = b.
(iii) If (x) is increasing function on (a , b), then tangent at every point on the curve y = f(x)
makes an acute angle θ with the positive direction of x-axis.
![]()
(iv) Let f be a differentiable real function defined on an open interval (a, b).
• If f ‗ (x) > 0 for all x ∈ (a, b), then f (x) is increasing on (a, b).
• If f ‗ (x) < 0 for all x ∈ (a , b), then f (x) is decreasing on (a, b).
(v) Let f be a function defined on (a, b).
• If f ‗(x) > 0 for all x ∈ (a, b) except for a finite number of points, where f ‗ (x) = 0, then f(x) is increasing on (a, b).
• If f ‗(x) < 0 for all x ∈ (a , b) except for a finite number of points, where f ‗(x) = 0, then f(x) is decreasing on (a , b).
1. If f(x)is strictly increasing function on an interval [a, b], then f-1 exist and also a strictly
increasing function.
2. If f(x) is strictly increasing function on [a, b], such that it is continuous, then f-1 is
continuous on [f(a), f(b)].
3. If f(x) and g(x) are strictly increasing (or decreasing) function on [a, b], then gof(x) is
strictly increasing (or decreasing) function on [a, b].
4. If one of the two functions f(x) and g(x) is strictly increasing and other a strictly
decreasing, then gof(x) is strictly decreasing on [a, b].
5. If f(x) is continuous on [a, b], such that f‘ (c) ≥ 0 (f ‗ (c) > 0) for each c ∈ (a, b) is strictly
increasing function on [a, b].
6. If f(x) is continuous on [a, b] such that f ‗(c) ≤ (f ‗ (c) < 0) for each c ∈ (a, b), then f(x) is
strictly decreasing function on [a, b].
1. A function y = f(x) is said to have a local maximum at a point x = a. If f(x) ≤ f(a) for all x ∈ (a – h, a + h), where h is somewhat small but positive quantity.
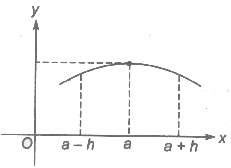
The point x = a is called a point of maximum of the function f(x) and f(a) is known as the maximum value or the greatest value or the absolute maximum value of f(x).
2. The function y = f(x) is said to have a local minimum at a point x = a, if f(x) ≥ f(a) for all x ∈ (a – h, a + h), where h is somewhat small but positive quantity.
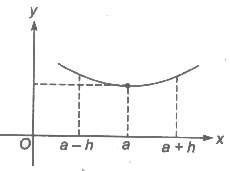
The point x = a is called a point of minimum of the function f(x) and f(a) is known as the minimum value or the least value or the absolute minimum value of f(x).
1. If f(x) is continuous function in its domain, then at least one maxima and one minima
must lie between two equal values of x.
2. Maxima and minima occur alternately, i.e., between two maxima there is one minima
and vice-versa.
3. If f(x) → ∞ as x → a or b and f ‗ (x) = 0 only for one value of x (sayc) between a and b,
then f(c) is necessarily the minimum and the least value.
4. If f(x) → p -∞ as x → a or b and f(c) is necessarily the maximum and the greatest value.
1. If f(x) be a differentiable functions, then f ‗(x) vanishes at every local maximum and at
every local minimum.
2. The converse of above is not true, i.e., every point at which f‘ (x) vanishes need not be a
local maximum or minimum. e.g., if f(x) = x3 then f ‗(0) = 0, but at x =0. The function
has neither minimum nor maximum. In general these points are point of inflection.
3. A function may attain an extreme value at a point without being derivable there at, e.g., f(x) = |x| has a minima at x = 0 but f’(0) does not exist.
4. A function f(x) can has several local maximum and local minimum values in an interval. Thus, the maximum and minimum values of f(x) defined above are not necessarily the
greatest and the least values of f(x) in a given interval.
5. A minimum value at some point may even be greater than a maximum values at some other point.
Let y = f(x) be a function defined on [a, b]. By a local maximum (or local minimum) value of a
function at a point c ∈ [a, b] we mean the greatest (or the least) value in the immediate
neighbourhood of x = c. It does not mean the greatest or absolute maximum (or the least
or absolute minimum) of f(x) in the interval [a, b].
A function may have a number of local
maxima or local minima in a given interval and even a local minimum may be greater than a
relative maximum.
A function f(x) is said to attain a local maximum at x = a, if there exists a neighbourhood (a –
δ, a + δ), of c such that, f(x) < f(a), ∀ x ∈ (a – δ, α + δ), x ≠ a or f(x) – f(a)< 0, ∀ x ∈ (a – δ, α + δ), x ≠ a
In such a case f(a) is called to attain a local maximum value of f(x) at x = a.
f (x) > f(a), ∀ x ∈ (a – δ, α + δ), x ≠ a or f(x) – f(a) > 0, ∀ x ∈ (a – δ, α + δ), x ≠ a
In such a case f(a) is called the local minimum value of f(x) at x = a.
Let f(x) be a differentiable function on an interval I and a ∈ I. Then,
1. (i) Point a is a local maximum of f(x), if
(a) f ‗(a) = 0
(b) f ‗(x) > 0, if x ∈ (a – h, a) and f‘ (x) < 0, if x ∈ (a, a + h), where h is a small but
positive quantity.
2. (ii) Point a is a local minimum of f(x), if
(a) f ‗(a) = 0
(b) f ‗(a) < 0, if x ∈ (a – h, a) and f ‗(x) > 0, if x ∈ (a, a + h), where h is a small but
positive quantity.
3. (iii) If f ‗(a) = 0 but f ‗(x) does not changes sign in (a – h, a + h), for any positive quantity h, then x = a is neither a point of minimum nor a point of maximum.
Let f(x) be a differentiable function on an interval I. Let a ∈ I is such that f ―(x) is continuous at x = a. Then,
1. x = a is a point of local maximum, if f ‗(a) = 0 and f ―(a) < 0.
2. x = a is a point of local minimum, if f ‗(a) = 0 and f‖(a) > 0.
3. If f ‗(a) = f ―(a) = 0, but f‖ (a) ≠ 0, if exists, then x = a is neither a point of local
maximum nor a point of local minimum and is called point of inflection.
4. If f ‗(a) = f ―(a) = f ‗‖(a) = 0 and f iv(a) < 0, then it is a local maximum. And if f iv > 0,
then it is a local minimum.
Let f be a differentiable function on an interval / and let a be an interior point of / such that
(i) f ‗(a) = f ―(a) = f ‗‖(a) = … f n – 1(a) = 0 and
(ii) fn (a) exists and is non-zero, then
• If n is even and f n (a) < 0 ⇒ x = a is a point of local maximum.
• If n is even and f n (a) > 0 ⇒ x = a is a point of local minimum.
• If n is odd ⇒ x = a is a point of local maximum nor a point of local minimum.
1. To Find Range of a Continuous Function Let f(x) be a continuous function on [a, b],
such that its least value in [a, b1 is m and the greatest value in [a, b] is M. Then, range of
value of f(x) for x ∈ [a, b] is [m, M].
2. To Check for the injectivity of a Function A strictly monotonic function is always oneone
(injective). Hence, a function f (x) is one-one in the interval [a, b], if f ‗(x) > 0 , ∀ x
∈ [a, b] or f‘ (x) < 0 , ∀ x ∈ [a, b].
3. The points at which a function attains either the local maximum value or local minimum
values are known as the extreme points or turning points and both local maximum and
local minimum values are called the extreme values of f(x). Thus, a function attains an
extreme value at x = a, if f(a) is either a local maximum value or a local minimum value.
Consequently at an extreme point ‗a‘, f (x) — f (a) keeps the same sign for all values of
x in a deleted nbd of a.
4. A necessary condition for (a) to be an extreme value of a function (x) is that f ‗(a) = 0 in case it exists.
5. This condition is only a necessary condition for the point x = a to be an extreme point. It is not sufficient. i.e., f ‗(a) = 0 does not necessarily imply that x = a is an extreme point.
There are functions for which the derivatives vanish at a point but do not have an extreme value. e.g., the function f(x) = x3 , f ‗(0) = 0 but at x = 0 the function does not attain an extreme value.
6. Geometrically the above condition means that the tangent to the curve y = f(x) at a point where the ordinate is maximum or minimum is parallel to the x-axis.
7. All x,for which f ‗(x) = 0, do not give us the extreme values. The values of x for which f ‗(x) = 0 are called stationary values or critical values of x and the corresponding values of f(x) are called stationary or turning values of f(x).
Points where a function f(x) is not differentiable and points where its derivative (differentiable coefficient) is z ?,ro are called the critical points of the function f(x).
Maximum and minimum values of a function f(x) can occur only at critical points. However, this does not mean that the function will have maximum or minimum values at all critical points. Thus, the points where maximum or minimum value occurs are necessarily critical Points but a function may or may not have maximum or minimum value at a critical point.
Consider function f(x) = x3. At x = 0, f ‗(x)= 0. Also, f ―(x) = 0 at x = 0. Such point is called point of inflection, where 2nd derivative is zero. Consider another function f(x) = sin x, f ―(x)= – sin x. Now, f ―(x)= 0 when x = nπ, then this points are called point of inflection.
1. It is not necessary that 1st derivative is zero.
2. 2nd derivative must be zero or 2nd derivative changes sign in the neighbourhood of point of inflection.
• Let y = f(x) be a given function with domain D.
• Let [a, b] ⊆ D, then global maximum/minimum of f(x) in [a, b] is basically the
greatest/least value of f(x) in [a, b].
• Global maxima/minima in [a, b] would always occur at critical points of f(x) with in [a,
b] or at end points of the interval.
In order to find the global maximum and minimum of f(x) in [a, b], find out all critical points of f(x) in [a, b] (i.e., all points at which f ‗(x)= 0) and let f(c1), f(c2) ,…, f(n) be the values of the function at these points.
Then, M1 → Global maxima or greatest value. and M1 → Global minima or least value.
where M1 = max { f(a), f(c1), f(c1) ,…, f(cn), f(b)}
and M1 = min { f(a), f(c1), f(c2) ,…, f(cn), f(b)}
Then, M1 is the greatest value or global maxima in [a, b] and M1 is the least value or global minima in [a, b].
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.