Determinants Class 12 Notes For Maths Chapter 4

NCERT Mathematics Notes for Class 12
Chapter 4: Determinants

Determinant

Every square matrix A is associated with a number, called its determinant and it is denoted by det (A) or |A| .

Only square matrices have determinants. The matrices which are not square do not have determinants

(i) First Order Determinant

If A = [a], then det (A) = |A| = a

(ii) Second Order Determinant

|A| = a₁₁a₂₂ – a₂₁a₁₂

(iii) Third Order Determinant

Evaluation of Determinant of Square Matrix of Order 3 by Sarrus Rule

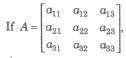
then determinant can be formed by enlarging the matrix by adjoining the first two columns on the right and draw lines as show below parallel and perpendicular to the diagonal.

The value of the determinant, thus will be the sum of the product of element. in line parallel to the diagonal minus the sum of the product of elements in line perpendicular to the line segment. Thus,

Δ = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ – a₁₃a₂₂a₃₁ – a₁₁a₂₃a₃₂ – a₁₂a₂₁a₃₃.
Note This method doesn’t work for determinants of order greater than 3.

Properties of Determinants

(i) The value of the determinant remains unchanged, if rows are changed into columns and columns are changed into rows e.g., |A’| = |A|
(ii) If A = [a_ij]_{n x n} , n > 1 and B be the matrix obtained from A by interchanging two of its rows or columns, then
det (B) = – det (A)
(iii) If two rows (or columns) of a square matrix A are proportional, then |A| = O.
(iv) |B| = k |A| ,where B is the matrix obtained from A, by multiplying one row (or column) of A by k.
(v) |kA| = kn|A|, where A is a matrix of order n x n.
(vi) If each element of a row (or column) of a determinant is the sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants, e.g.,

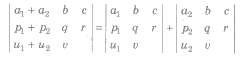
(vii) If the same multiple of the elements of any row (or column) of a determinant are added to the corresponding elements of any other row (or column), then the value of the new determinant remains unchanged, e.g.,

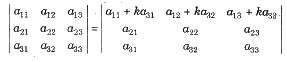
(viii) If each element of a row (or column) of a determinant is zero, then its value is zero.
(ix) If any two rows (columns) of a determinant are identical, then its value is zero.
(x) If each element of row (column) of a determinant is expressed as a sum of two or more terms, then the determinant can be expressed as the sum of two or more determinants.

Important Results on Determinants

(i) |AB| = |A||B| , where A and B are square matrices of the same order.
(ii) |Aⁿ| = |A|ⁿ
(iii) If A, B and C are square matrices of the same order such that ith column (or row) of A is the sum of i th columns (or rows) of B and C and all other columns (or rows) of A, Band C are identical, then |A| =|B| + |C|
(iv) |I_n| = 1,where I_n is identity matrix of order n
(v) |O_n| = 0, where O_n is a zero matrix of order n
(vi) If Δ(x) be a 3rd order determinant having polynomials as its elements.
(a) If Δ(a) has 2 rows (or columns) proportional, then (x – a) is a factor of Δ(x).
(b) If Δ(a) has 3 rows (or columns) proportional, then (x – a)² is a factor of Δ(x). ,
(vii) A square matrix A is non-singular, if |A| ≠ 0 and singular, if |A| =0.
(viii) Determinant of a skew-symmetric matrix of odd order is zero and of even order is a nonzero perfect square.
(ix) In general, |B + C| ≠ |B| + |C|
(x) Determinant of a diagonal matrix = Product of its diagonal elements
(xi) Determinant of a triangular matrix = Product of its diagonal elements
(xii) A square matrix of order n, is non-singular, if its rank r = n i.e., if |A| ≠ 0, then rank (A) = n

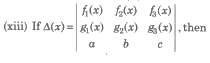
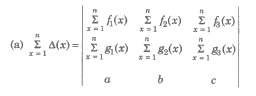
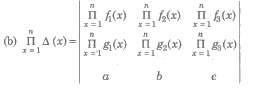
(xiv) If A is a non-singular matrix, then |A^-1| = 1 / |A| = |A|^-1
(xv) Determinant of a orthogonal matrix = 1 or – 1.
(xvi) Determinant of a hermitian matrix is purely real .
(xvii) If A and B are non-zero matrices and AB = 0, then it implies |A| = 0 and |B| = 0.

Minors and Cofactors

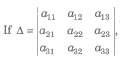
then the minor M_ij of the element a_ij is the determinant obtained by deleting the i row and jth column.

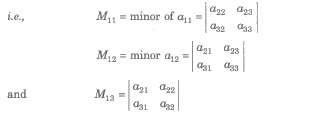
The cofactor of the element a_ij is C_ij = (- 1)i + j M_ij

Adjoint of a Matrix :-

Adjoint of a matrix is the transpose of the matrix of cofactors of the give matrix, i.e.,

Properties of Minors and Cofactors

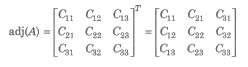
(i) The sum of the products of elements of .any row (or column) of a determinant with the cofactors of the corresponding elements of any other row (or column) is zero, i.e., if

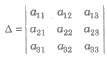
then a₁₁C₃₁ + a₁₂C₃₂ + a₁₃C₃₃ = 0 ans so on.
(ii) The sum of the product of elements of any row (or column) of a determinant with the cofactors of the corresponding elements of the same row (or column) is Δ

Differentiation of Determinant

Integration of Determinant

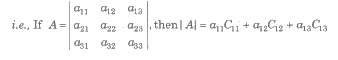
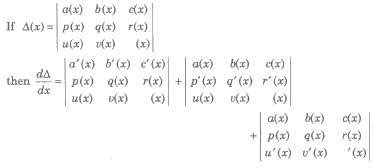
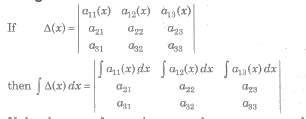
If the elements of more than one column or rows are functions of x, then the integration can be
done only after evaluation/expansion of the determinant.

Solution of Linear equations by Determinant/Cramer’s Rule

Case 1.

The solution of the system of simultaneous linear equations
a₁x + b₁y = C₁ …(i)
a₂x + b₂y = C₂ …(ii)
is given by x = D₁ / D, Y = D₂ / D

(i) If D ≠ 0, then the given system of equations is consistent and has a unique solution given by x = D₁ / D, y = D₂ / D
(ii) If D = 0 and Dl = D2 = 0, then the system is consistent and has infinitely many solutions.
(iii) If D = 0 and one of Dl and D2 is non-zero, then the system is inconsistent.

Case II.

Let the system of equations be
a1x + b1y + C1z = d1
a2x + b2y + C2z = d2
a3x + b3y + C3z = d3
Then, the solution of the system of equation is x = D1 / D, Y = D2 / D, Z = D3 / D, it is called Cramer’s rule.

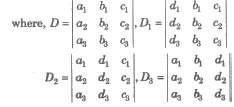
(i) If D ≠ 0, then the system of equations is consistent with unique solution.
(ii) If D = 0 and atleast one of the determinant D₁, D₂, D₃ is non-zero, then the given system is inconsistent, i.e., having no solution.
(iii) If D = 0 and D₁ = D₂ = D₃ = 0, then the system is consistent, with infinitely many solutions.
(iv) If D ≠ 0 and D₁ = D₂ = D₃ = 0, then system has only trivial solution, (x = y = z = 0).

Cayley-Hamilton Theorem

Every matrix satisfies its characteristic equation, i.e., if A be a square matrix, then |A – xl| = 0 is the characteristics equation of A. The values of x are called eigenvalues of A.
i.e., if x₃ – 4x₂ – 5x – 7 = 0 is characteristic equation for A, then A₃ – 4A₂ + 5A – 7I = 0

Properties of Characteristic Equation

(i) The sum of the eigenvalues of A is equal to its trace.
(ii) The product of the eigenvalues of A is equal to its determinant.
(iii) The eigenvalues of an orthogonal matrix are of unit modulus.
(iv) The feigen values of a unitary matrix are of unit modulus.
(v) A and A’ have same eigenvalues.
(vi) The eigenvalues of a skew-hermitian matrix are either purely imaginary or zero.
(vii) If x is an eigenvalue of A, then x is the eigenvalue of A^* .
(viii) The eigenvalues of a triangular matrix are its diagonal elements.
(ix) If x is the eigenvalue of A and |A| ≠ 0, then (1 / x) is the eigenvalue of A^-1.
(x) If x is the eigenvalue of A and |A| ≠ 0, then |A| / x is the eigenvalue of adj (A).
(xi) If x₁, x₂,x₃, … ,x_n are eigenvalues of A, then the eigenvalues of A² are x₂ ², x₂ ²,…, x_n ².

Cyclic Determinants

Applications of Determinant in Geometry

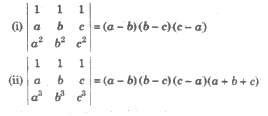
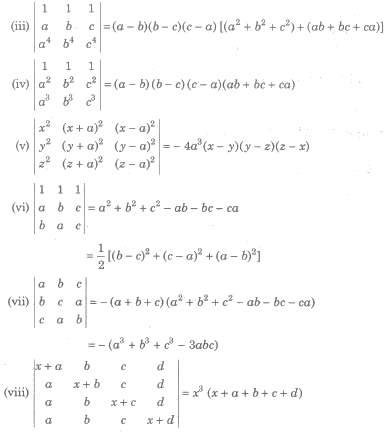
Let three points in a plane be A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃), then

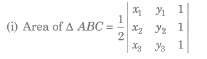
= 1 / 2 [x₁ (y₂ – y3) + x₂ (y3 – y₁) + x3 (y₁ – y₂)]

Maximum and Minimum Value of Determinants

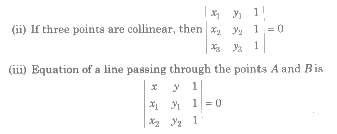
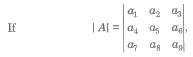
where a_is ∈ [α₁, α₂,…, α_n]
Then, |A|_max when diagonal elements are
{ min (α₁, α₂,…, α_n)}
and non-diagonal elements are
{ max (α₁, α₂,…, α_n)}
Also, |A|_min = – |A|_max

Ncert Solution for class 6 to 12 download in pdf

Follow Us On

Facebook

Twitter

Youtube

Linkdin