Differential Equations Class 12 Notes For Maths Chapter 9

NCERT Mathematics Notes for Class 12
Chapter 9. Differential Equations

An equation that involves an independent variable, dependent variable and differential coefficients of dependent variable with respect to the independent variable is called a differential equation.
e.g.,
(i) x²(d²y / dx²) + x³ (dy / dx)³ 7x²y²
(ii) (x² + y²) dx = (x² – y²) dy

Order and Degree of a Differential Equation

The order of a differential equation is the order of the highest derivative occurring in the equation. The order of a differential equation is always a positive integer.

The degree of a differential equation is the degree (exponent) of the derivative of the highest order in the equation, after the equation is free from negative and fractional powers of the derivatives.

Linear and Non-Linear Differential Equations

A differential equation is said to be linear, if the dependent variable and all of its derivatives occurring in the first power and there are no product of these. A linear equation of nth order can be written in the form

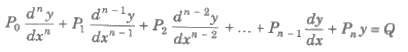
where, P₀, P₁, P₂,…, P_{n – 1} and Q must be either constants or functions of x only.
A linear differential equation is always of the first degree but every differential equation of the first degree need not be linear.
e.g., The equations d²y / dx² + (dy / dx)² + xy = 0 and x(d²y / dx²) + y (dy / dx) + y = x³, (dy / dx) d²y / dx² + y = 0 are not linear.

Solution of Differential Equations

A solution of a differential equation is a relation between the variables, not involving the differential coefficients, such that this relation and the derivative obtained from it satisfy the given differential equation.
e.g., Let d²y / dx² + y = 0

Integrating above equation twicely, we get y = A cos x + B sin x.

General Solution

If the solution of the differential equation contains as many independent arbitrary constants as the order of the differential equation, then it is called the general solution or the complete integral of the differential equation.

e.g., The general solution of d²y / dx² + y = 0 is y = A cos x + B sin x because it contains two arbitrary constants A and B, which is equal to the order of the equation.

Particular Solution

Solution obtained by giving particular values to the arbitrary constants in the general solution is called a particular solution. e.g., In the previous example, if A = B = 1, then y = cos x + sin x is a particular solution of the differential equation d²y / dx² + y = 0.

Solution of a differential equation is also called its primitive.

Formation of Differential Equation

Suppose, we have a given equation with n arbitrary constants f(x, y, c₁, c₂,…, c_n) = 0.
Differentiate the equation successively n times to get n equations.
Eliminating the arbitrary constants from these n + 1 equations leads to the required differential equations.

Solutions of Differential Equations of the First Order and First Degree

A differential equation of first degree and first order can be solved by following method.

1. Inspection Method

If the differential equation’ can be written as f [f₁(x, y) d {f₁(x, y)}] + φ [f₂(x, y) d {f₂(x, y)}] +… = 0] then each term can be integrated separately.

For this, remember the following results

2. Variable Separable Method

If the equation can be reduced into the form f(x) dx + g(y) dy = 0, we say that the variable have been separated. On integrating this reduced, form, we get ∫ f(x) dx + ∫ g(y) dy = C, = C, where C is any arbitrary constant.

3. Differential Equation Reducible to Variables Separable Method

A differential equation of the form dy / dx = f(ax + by + c) can be reduced to variables separable form by substituting ax + by + c = z => a + b dy / dx = dz / dx
The given equation becomes 1 / b (dz / dx – a) f(z) => dz / dx = a + b f(z) => dz / a+ bf(z) = dx
Hence, the variables are separated in terms of z and x.

4. Homogeneous Differential Equation

A function f(x, y) is said to be homogeneous of degree n, if f(λx, λy) = λⁿ f(x, y) Suppose a differential equation can be expressed in the form dy / dx = f(x, y) / g(x, y) = F (y / x)
where, f(x, y) and g(x, y) are homogeneous function of same degree. To solve such types of equations, we put y = vx
=> dy / dx = v + x dv / dx.
The given equation, reduces to v + x dv / dx = F(v) => x dv / dx = F(v) – v
∴ dv / F(v) – v = dx / x Hence, the variables are separated in terms of v and x.

5. Differential Equations Reducible to Homogeneous Equation

The differential equation of the form dy / dx = a^₁x + b^₁y + c^₁ / a₂x + b₂y + c₂ …… (i)
put X = X + h and y = Y + k
∴ dY / dX = a^₁ X + b^₁ Y + (a^₁h + b^₁k + c^₁) / a₂X + b₂ Y + (a₂h + b₂k + c₂) ……(ii)
We choose h and k, so as to satisfy a^₁h + b^₁k + c^₁ = 0 and a₂h + b₂k + c₂ = 0.
On solving, we get h / b^₁c₂ – b₂c^₁ = k / c^₁a₂ – c₂a^₁ = ^₁ / a^₁b₂ – a₂b^₁
∴ h = b^₁c₂ – b₂c^₁ / a^₁b₂ – a₂b^₁ and k = c^₁a₂ – c₂a^₁ / a^₁b₂ – a₂b^₁

Provided a₁b₂ – a₂b₁ ≠ 0 , a₁ / a₂ ≠ ba / b₂

Then, Eq, (ii) reduces to dY / dX = (a₁ X + b₁ Y) / (a₂X + b₂ Y), which is a homogeneous form and will be solved easily.

6. Exact Differential Equation

Differential equation M(x,y) dy + N(x,y) dy = 0 is called an exact differential equation.
If a function u (x, y) exist such that, du = Mdx + Ndy.

Necessary and Sufficient Condition for an Equation to be an Exact Differential Equation

Differential equation Mdx + Ndy = 0 where, M and N are the functions •of x and y, will be an exact differential equation, if∂N / ∂y = ∂N / ∂x

Solution of Exact Differential Equation

7. Linear Differential Equation

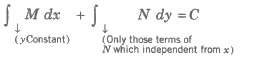
A linear differential equation of the first order can be either of the following forms
(i) dy / dx + Py = Q, where P and Q are functions of x or constants.
(ii) dx / dy + Rx = S, where Rand S are functions of y or constants.
Consider the differential Eq. (i) i.e., dy / dx + Py = Q

Similarly, for the second differential equation dx / dy + Rx = S, the integrating factor, IF = e ∫^{R dy} and the general solution is

x (IF) = ∫ S (IF) dy + C

8. Differential Equation Reducible to Linear Form

Bernoulli’s Equation An equation of the form dy / dx + Py = Qyⁿ, where P and Q are functions of x along or constants, is called Bernoulli’s equation.
Divide both the sides by yⁿ, we get y^-n dy / dx + Py^{-n + 1}
= Q Put y^{-n + 1}
= z => (-n + 1)y-n dy / dx
= dz / dx
The equation reduces to
1 / 1 – n dz / dx + Pz = Q => dz / dx + (1 – n) Pz = Q (1 – n) which is linear in z and can be solved in the usual manner.

9. Clairaut Form for Differential Equation

Differential equation y = Px + f(p), where P= dy / dx … (i) is called clairaut form of differential equation. In which, get its general solution by replacing P from C.
Now, differential on both sides of Eq, (i) with respect to x and put dy / dx = P.
P = P + x dp / dx + f’ (P) dp / dx = 0
=> [x + f’ (p)] dp / dx = 0
=> dp / dx = 0 => p = C

10. Orthogonal Trajectory

Any curve, which cuts every member of a given family of curves at right angle, is called anorthogonal trajectory of the family.

Procedure for finding the Orthogonal Trajectory

(i) Let f(x,y,c)= 0 be the equation of the given family of curves, where ‘c’ is an arbitrary parameter.
(ii) Differentiate f = 0, with respect to ‘x’ and eliminate 0, i.e., from a differential equation.
(iii) Substitute (- dx / dy) for (dy / dx) in the above differential equation. This will give the differential equation of the orthogonal trajectories.
(iv) By solving this differential equation, we get the required orthogonal trajectories.

Ncert Solution for class 6 to 12 download in pdf

Follow Us On

Facebook

Twitter

Youtube

Linkdin