types of triangles similar congruent properties different angles , triangles 10 notes, class 10 maths notes, triangles class 10, triangles class 10 notes, class 10 triangles, note maths, maths notes, triangles, class 10 cmaths chapter 6 notes, 10th standard maths notes, 10th std maths notes, class 10 maths notes chapter 6, triangles chapter class 10 notes
1. Similar Triangles:- Two triangles are said to be similar, if
(a) their corresponding angles are equal
and
(b) their corresponding sides are in proportion (or are in the same ration).
2. Basic proportionality Theorem [ or Thales theorem ].
3. Converse of Basic proportionality Theorem.
4. Criteria for similarity of Triangles.
(a) AA or AAA similarity criterion.
(b) SAS similarity criterion.
(c) SSS similarity criterion.
5. Areas of similar triangles.
6. Pythagoras theorem.
7. Converse of Pythagoras theorem
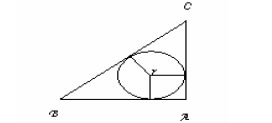
1. ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The
lengths of the two sides containing the right angle are 6cm and 8 cm. Find the
radius of the in circle.
(Ans: r=2)
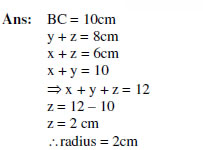
2. ABC is a triangle. PQ is the line segment intersecting AB in P and AC in Q such that PQ parallel to BC and divides triangle ABC into two parts equal in area. Find BP: AB.
Ans: Refer example problem of text book.
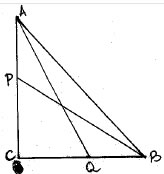
3. In a right triangle ABC, right angled at C, P and Q are points of the sides CA and
CB respectively, which divide these sides in the ratio 2: 1.
Prove that
9AQ2= 9AC2 +4BC2
9BP2= 9BC2 + 4AC2
9 (AQ2+BP2) = 13AB2
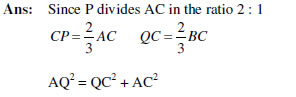
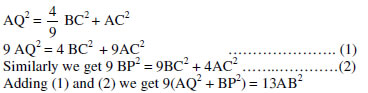
4. P and Q are the mid points on the sides CA and CB respectively of triangle ABC right angled at C. Prove that 4(AQ2 +BP2) = 5AB2
5. In an equilateral triangle ABC, the side BC is trisected at D.
Prove that 9AD2 = 7AB2
6. There is a staircase as shown in figure connecting points A and B. Measurements
of steps are marked in the figure. Find the straight distance between A and B.
(Ans:10)
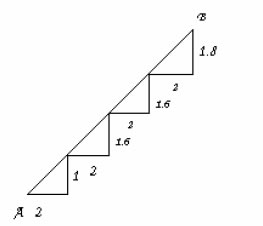
Ans: Apply Pythagoras theorem for each right triangle add to get length of AB.
7. Find the length of the second diagonal of a rhombus, whose side is 5cm and one of
the diagonals is
6cm. (Ans: 8cm)
Ans: Length of the other diagonal
= 2(BO)
where BO = 4cm
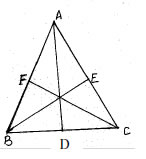
8. Prove that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
Ans: To prove 3(AB2 + BC2 + CA2) = 4 (AD2+ BE2 + CF2)
In any triangle sum of squares of any two sides is equal to twice the square of half
of third side, together with twice the square of medianbisecting it
.
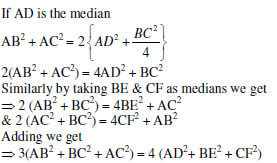
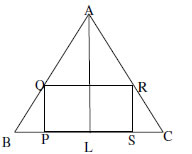
9. ABC is an isosceles triangle is which AB=AC=10cm.BC=12. PQRS is a rectangle inside the isosceles triangle. Given PQ=SR= y cm, PS=QR=2x. Prove
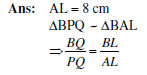
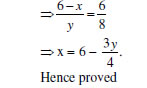
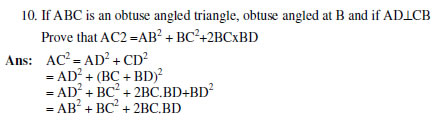
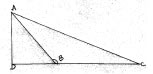
11. If ABC is an acute angled triangle , acute angled at B and
prove that AC2 =AB2 + BC2 −2BC × BD
Ans: Proceed as sum no. 10.
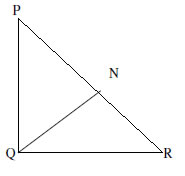
12. Prove that in any triangle the sum of the squares of any two sides is equal to twice the square of half of the third side together with twice the square of the median, which bisects the third side.
13. If A be the area of a right triangle and b one of the sides containing the right
angle, prove that the length of the altitude on the hypotenuse is
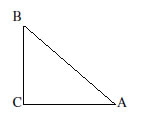
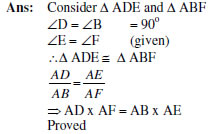
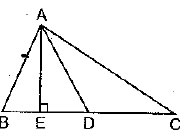
16. In the given figure, 
and E is the mid-point of CA. Prove that
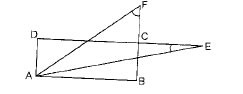
17. ABCD is a parallelogram in the given figure, AB is divided at P and CD and Q so
that AP:PB=3:2 and CQ:QD=4:1. If PQ meets AC at R, prove that AR
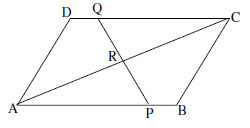
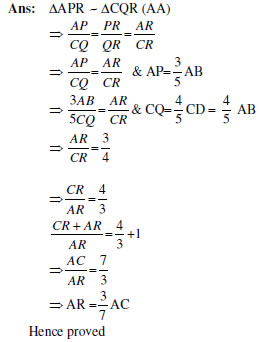
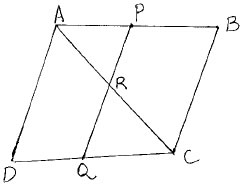
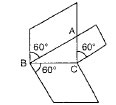
18. Prove that the area of a rhombus on the hypotenuse of a right-angled triangle, with one of the angles as 60o, is equal to the sum of the areas of rhombuses with one of their angles as 60o drawn on the other two sides.
19. An aeroplane leaves an airport and flies due north at a speed of 1000 km/h. At the
same time, another plane leaves the same airport and flies due west at a speed of 1200
km/h. How far apart will be the two planes after 1½ hours. 
20. ABC is a right-angled isosceles triangle, right-angled at B. AP, the bisector of
, intersects BC at P. Prove that
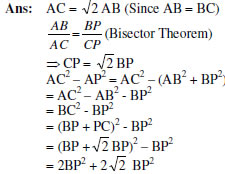
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.
