
real numbers, properties of real numbers, real numbers definition, real numbers examples , real numbers 10 notes, class 10 maths notes, real numbers class 10, real numbers class 10 notes, class 10 real numbers, note maths, maths notes, real numbers, class 10 cmaths chapter 1 notes, 10th standard maths notes, 10th std maths notes, class 10 maths notes chapter 1, real numbers chapter class 10 notes
1. Euclid’s Division lemma:- Given Positive integers a and b there exist unique integers q and r
satisfying
a=bq +r, where 0 ![]() where a, b, q and r are respectively called as dividend, divisor, quotient and
remainder.
where a, b, q and r are respectively called as dividend, divisor, quotient and
remainder.
2. Euclid’s division Algorithm:- To obtain the HCF of two positive integers say c and d, with c>0, follow the steps below:
Step I: Apply Euclid’s division lemma, to c and d, so we find whole numbers, q and r such that c =dq+r, 0![]()
Step II: If r=0, d is the HCF of c and d. If r![]()
Step III: Continue the process till the remainder is zero. The divisor at this stage will be the required
HC
3. The Fundamental theorem of Arithmetic:-
Every composite number can be expressed ( factorised ) as a product of primes, and this
factorization is unique, apart from the order in which the prime factors occur.
Ex.:![]()
Theorem: LET![]() be a rational number whose decimal expansion terminates. Then
be a rational number whose decimal expansion terminates. Then![]() can be
expressed in the form
can be
expressed in the form

1. If the H C F of 657 and 963 is expressible in the form of 657x + 963x - 15 find x.Definition
(Ans:x=22)

2. Express the GCD of 48 and 18 as a linear combination. (Ans: Not unique)
 |
|
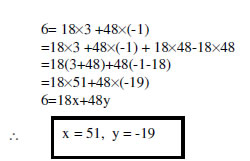
Hence, x and y are not unique.
3. Prove that one of every three consecutive integers is divisible by 3.
Ans:
n,n+1,n+2 be three consecutive positive integers
We know that n is of the form 3q, 3q +1, 3q + 2
So we have the following cases Properties
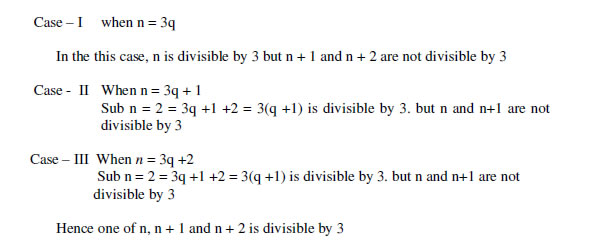
4. Find the largest possible positive integer that will divide 398, 436, and 542 leaving
remainder 7, 11, 15 respectively.
(Ans: 17)
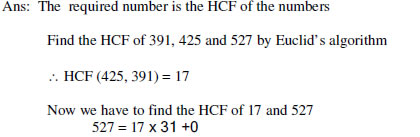
![]()
5. Find the least number that is divisible by all numbers between 1 and 10 (both
inclusive).
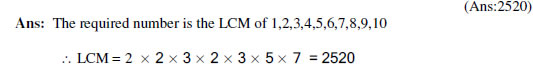
6. Show that 571 is a prime number.
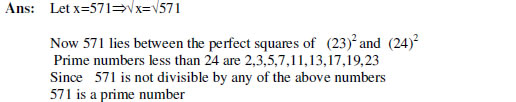
7. If d is the HCF of 30, 72, find the value of x & y satisfying d = 30x + 72y.

Hence, x and y are not unique
8. Show that the product of 3 consecutive positive integers is divisible by 6.
Ans: Proceed as in question sum no. 3
9. Show that for odd positive integer to be a perfect square, it should be of the form

11. If a and b are positive integers. Show that![]() always lies between
always lies between![]()
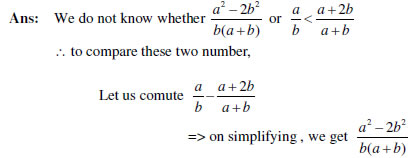
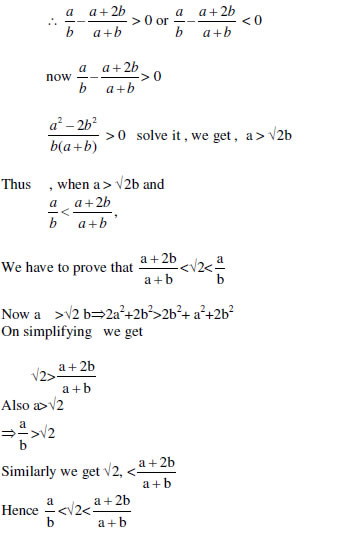
12. Prove that![]() is irrational, for every n
is irrational, for every n![]() N Symbol chart
N Symbol chart
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.