
volume and surface area class 9 notes for class 9 formulas download pdf, volume of cylinder, how to calculate the cylinder volume, cylinder volume unit, how to calculate the volume of the cylinder, volume of a section of a cylinder , surface areas and volumes 9 notes, class 9 maths notes, surface areas and volumes class 9, surface areas and volumes class 9 notes, class 9 surface areas and volumes, note maths, maths notes, surface areas and volumes, class 9 cmaths chapter 13 notes, 9th standard maths notes, 9th std maths notes, class 9 maths notes chapter 13, surface areas and volumes chapter class 9 notes
The bodies occupying space (i.e. have 3-dimension) are called solids such as a
cuboid, a cube, a cylinder, a cone, a sphere etc.
The measure of space occupied by a solid-body is
called its volume. The units of volume are cubic centimeters (written as cm3) or cubic meters
(written as m3).
CUBOID: A solid bounded by six rectangular faces is called a cuboid.
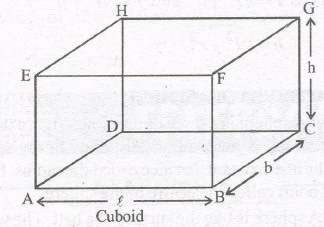
In the given figure, ABCDEFGH is a cuboid whose
(i) 6 faces are : ABCD, EFGH, ABFE, CDHQ ADHE, and BCGF Out of these, the four faces namely ABFE,
DCGH, ADHE and BCGF are called lateral faces of the cuboid.
(ii) 12 edges are : AB, BC, CD, DA, EF, FG GH, HE, CG BF, AE and DH
(iii) 8 vertices are : A, B, C, D, E, F, and H.
Remark : A rectangular room is in the form of a cuboid and its 4 walls are its lateral surfaces.
Cube : A cuboid whose length, breadth and height are all equal, is called a cube.
A cube has 6 faces, each face is square, 12 edges, all edges are of equal lengths and 8 vertices.
Let us consider a cuboid of length = 1 units
Breadth = b units and height = h units
Then we have :
(i) Total surface area of the cuboid
=2(l * b + b * h + h * l) sq. units
(ii) Lateral surface area of the cuboid
= [2 (1 + b)* h] sq. units
(iii) Area of four walls of a room = [2 (1 + b)* h] sq. units.
= (Perimeter of the base * height) sq. units
(iv) Surface area of four walls and ceiling of a room
= lateral surface area of the room + surface area of ceiling
=2(1+b)*h+l*b
(v) Diagonal of the cuboid = √l2 + b2 + h2
Consider a cube of edge a unit.
(i) The Total surface area of the cube = 6a2 sq. units
(ii) Lateral surface area of the cube = 4a2 sq. units.
(iii) The diagonal of the cube = √3 a units.
Cylinder: Solids like circular pillars, circular pipes, circular pencils, road rollers and gas
cylinders etc. are said to be in cylindrical shapes.
Curved surface area of the cylinder
= Area of the rectangular sheet
= length * breadth
= Perimeter of the base of the cylinder * height
= 2πr * h
Therefore, curved surface area of a cylinder = 2πrh
Total surface area of the cylinder =2πrh + 2πr2
So total area of the cylinder=2πr(r + h)
Remark : Value of TE approximately equal to 22 / 7 or 3.14.
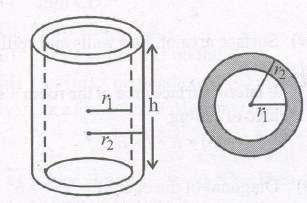
If a cylinder is a hollow cylinder whose inner radius is r1 and outer radius r2 and height h then
Total surface area of the cylinder
= 2πr1h + 2πr2h + 2π(r2
2 – r2
1)
= 2π(r1 + r2)h + 2π (r2 + r1) (r2 – r1)
= 2π(r1 + r2) [h + r2 – r1
A figure generated by rotating a right triangle about a perpendicular side is called the right
circular cone.
SURF
curved surface area of a cone = 1 / 2 * l * 2πr = πrl
where r is base radius and l its slant height
Total surface area of the right circular cone
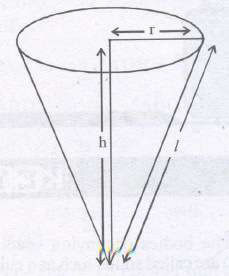
= curved surface area + Area of the base
= πrl + πr2 = πr(l + r)
Note : l2 = r2 + h2
By applying Pythagorus
Theorem, here h is the height of the cone.
Thus l = √r2 + h2 and r
= √l2 – h2
h
= √l2 + r2
Sphere: A sphere is a three dimensional figure (solid figure) which is made up of all points in
the space which lie at a constant distance called the radius, from a fixed point called the centre
of the sphere.
Note : A sphere is like the surface of a ball. The word solid sphere is used for the solid whose
surface is a sphere.
Surface area of a sphere: The surface area of a sphere of radius r
= 4 x area of a circle of radius
r
= 4 * πr2
= 4πr2
Surface area ofa hemisphere
= 2πr2
Total surface area of a hemisphere
= 2πr2 + πr2
= 3πr2
Total surface area of a hollow hemisphere with inner and outer radius r1 and r2 respectively
= 2πr2
1 + 2πr2
2 + π(r2
2 — r2
1)
= 2π(r2
1 + r2
2) + π(r2
2 —r2
1)
Volume : Solid objects occupy space.
The measure of this occupied space is called volume of the object.
Capacity of a container : The capacity of an object is the volume of the substance its interior
can accommodate.
The unit of measurement of either of the two is cubic unit.
Volume of a cuboid : Volume of a cuboid =Area of the base * height V=l * b * h
So, volume of a cuboid = base area * height = length * breadth * height
Volume of a cube : Volume of a cube = edge * edge * edge
= a3
where a
= edge of the cube
Volume of a cylinder = πr2h
volume of the hollow cylinder πr2
2h — πr2
1h
= π(r2
2 – r2
1)h
volume of a cone = 1 / 3 πr2h,
where r is the base radius
and h is the height of the cone.
VOLUME OF A SPHERE
volume of a sphere the sphere = 4 / 3 πr3, where r is the radius of the sphere.
Volume of a hemisphere = 2 / 3 πr3
Volume of the material of a hollow sphere with inner and outer radii r1 and
r2 respectively
= 4 / 3 πr3
2 – 4 / 3 πr3
1
= 4 / 3π(r3
2 – r3
1)
Volume of the material of a hemisphere with inner and
outer radius r1 and r2 respectively
= 2 / 3π(r3
2 – r3
1)
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.