Areas of Parallelograms and Triangles Class 9 Notes For Maths Chapter 9

Areas of Parallelograms and Triangles

Notes For Class 9 Formulas Download PDF

INTRODUCTION

You may recall that the part of the plane enclosed by a simple figure is called a planar region corresponding to that figure. The magnitude or measure of this lanar region is called its area.

We are also familiar with the concept of congruent figures.

Two figures are called congruent, if they have the same shape and the same size.

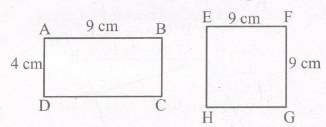
So if two figures A and B are congruent they must have equal areas. However, the converse of this statement is not true. In other words, two figures having equal areas need not be congruent. For example, in figure, rectangles ABCD and EFGH have equal areas (9 x 4 cm2 and 6 x 6 cm2) but clearly they are not congruent.

FIGURES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS

Two figures are said to be on the same ‘base add between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.

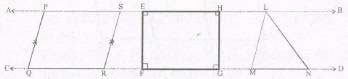
If a parallelogram PQRS, a rectangle EFGH and a triangle LMN are so drawn that their bases lie on a straight line (say, CD) and their other vertices lie on a line AB parallel to it (CD), then the parallelogram, the rectangle and the triangle are said to be between the same parallels.

Note : Out of the two parallels, one must be the line containing the common base. ΔABC and ΔDBE of figure are not on the common base.

PARALLELOGRAMS ON THE SAME BASE AND BETWEEN THE SAME PARALLELS.

Statement : Parallelograms on the same base and between the same parallels are equal in area.

Remark: Area of a parallelogram is the product of its any side and the corresponding altitude.

Statement : if a triangle an a a parallelog Ain Are mit* same base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.

TRIANGLES ON THE SAME BASE AND BETWEEN THE SAME PARALLELS

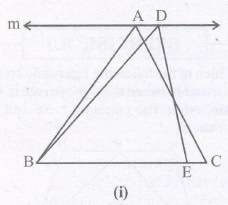
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

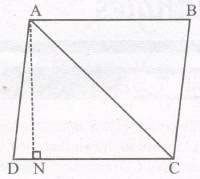
Note : Area of ΔADC = 1/2 x base DC x corresponding altitude AN

In other words, area of a triangle is half the product of its base (or any side) and the corresponding altitude (or height).

Remarks : Two triangles with same base (or equal bases) and equal areas will have equal corresponding altitudes.

Theorem : Two triangles having the same base (or equal bases) and equal areas lie between the same parallels.

Ncert Solution for class 6 to 12 download in pdf

Follow Us On

Facebook

Twitter

Youtube

Linkdin