9th class maths formulas cbse notes chapter 1 number system , number system 9 notes, class 9 maths notes, number system class 9, number system class 9 notes, class 9 number system, note maths, maths notes, number system, class 9 cmaths chapter 1 notes, 9th standard maths notes, 9th std maths notes, class 9 maths notes chapter 1, number system chapter class 9 notes
• Natural numbers are - 1, 2, 3, …………….. denoted by N.
• Whole numbers are - 0, 1, 2, 3, ……………… denoted by W.
• Integers - ……. -3, -2, -1, 0, 1, 2, 3, ……………… denoted by Z.
• Rational numbers - All the numbers which can be written in the form p/q,q ≠0 are called rational numbers where p and q are integers.
• Irrational numbers - A number s is called irrational, if it cannot be written in the form p/q where p and q are integers and q ≠0
• The decimal expansion of a rational number is either terminating or non terminating recurring. Thus we say that a number whose decimal expansion is either terminating or non terminating recurring is a rational number.
• The decimal expansion of a irrational number is non terminating non recurring.
• All the rational numbers and irrational numbers taken together.
• Make a collection of real number.
• A real no is either rational or irrational.
• If r is rational and s is irrational then r+s, r-s, r.s are always irrational numbers but r/s may be rational or irrational.
• Every irrational number can be represented on a number line using Pythagoras theorem.
• Rationalization means to remove square root from the denominator.
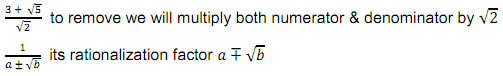
Section - A
Q.1 Is zero a rational number? Can you write in the form p/q, where p and q are integer and 
?
Q.2 Find five rational numbers between 
Q.3 State whether the following statements are true or false give reasons for your answers.
(i) Every natural no. is whole number.
(ii) Every integer is a whole number.
(iii) Every rational number is a whole number.
(iv) Every irrational number is a real number.
(v) Every real number is an irrational number.
(vi) Every point on the number line is of the form where 
is a natural no’s.
Q.4 Show how 
can be represented on the number line?
Q.5 Find the decimal expansion of 
? What kind of decimal expansion each has.
Q.6 Show that 1.272727 =
can be expressed in the form p/q, where p and q are integers and
Q.7 Write three numbers whose decimal expressions are non-terminating & non recurring?
Q.8 Find three different rational between 3/5 and 4/7.
Q.9 Classify the following numbers as rational or irrational.
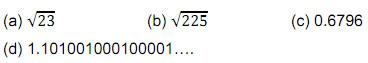
Section - C
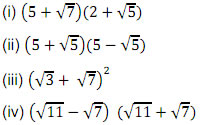
Q.13 Rationalize the denominator of 
Section - D
Q.1 Represent 
on number line.
Q.2 Recall, π is defined as the ratio of the circumference (say c) of a circle to its
diameter (say d). That is . This seems to contradict the fact that is irrational. How will you resolve this contradiction?
Q.3 Simplify
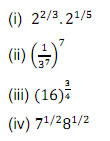
Q.1 Write the value of
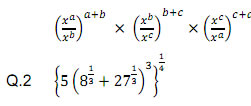
Q.3 If a & b are rational number, find the value of a & b in each of the following equalities.
Q.4 Prove that is an irrational number using long division method?
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.
