
quadrilaterals class 9 maths notes download in pdf, what is quadrilateral, quadrilatéral, about quadrilaterals, define quadrilateral, information on quadrilaterals, understanding quadrilaterals, golden quadrilateral, kinds of quadrilaterals, what is a quadrilateral, information about quadrilaterals, quadrilateral meaning, what are quadrilaterals, meaning of quadrilateral, history of quadrilaterals, what is quadrilaterals, classification of quadrilaterals, project on quadrilaterals, concyclic qua, quadrilaterals 9 notes, class 9 maths notes, quadrilaterals class 9, quadrilaterals class 9 notes, class 9 quadrilaterals, note maths, maths notes, quadrilaterals, class 9 cmaths chapter 8 notes, 9th standard maths notes, 9th std maths notes, class 9 maths notes chapter 8, quadrilaterals
A quadrilateral is a closed figure obtained by joining four point (with no three points collinear)
in an order.
Every quadrilateral has :
(i) Four vertices
(ii) Four sides
(iii) Four angles
(iv) Two
diagonals
Statement: The sum of the angles ofa quadrilateral is 360°
1. Trapezium : It is quadrilateral in which one pair of opposite sides are parallel.
2. Parallelogram : It is a quadrilateral in which both the pairs of opposite sides are parallel.
3. Rectangle : It is a quadrilateral whose each angle is 90°. ABCD is a rectangle.
(i) ∠A+ ∠B = 90° + 90° = 180° ⇔ AD || BC
(ii) ∠B+ ∠C= 900 + 900 = 180° ⇔ AB || DC
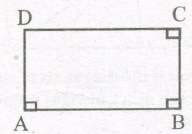
Rectangle ABCD is a parallelogram also.
4. Rhombus : It is a quadrilateral whose all the sides are equal.
5. Square : It is a quadrilateral whose all the sides are equal and each angle is 90°.
6. Kite : It is a quadrilateral in which two pairs of adjacent sides are equal.
Note :
• Square, rectangle and rhombus are all parallelograms.
•Kite and trapezium are not parallelograms.
• A square is a rectangle.
• A square is a rhombus
• A parallelogram is a trapezium.
A parallelogram is a quadrilateral in which opposite sides are parallel. It is denoted by
![]()
1. A diagonal of a parallelogram divides it into two congruent triangles.
2. The opposite sides of a parallelogram are equal.
Theorem : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
3. The opposite angles of a parallelogram are equal.
Theorem : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
4. The diagonals of a parallelogram bisect each other.
Theorem : If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
PROPORTIONALITY THEOREM)
Statement 1:
The line segment joining the mid-points of any two sides of a triangle is parallel to the third
side
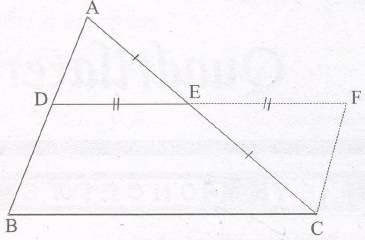
Statement 2:
The line drawn through the mid-point of one side of a triangle, parallel to another side bisects
the third side.
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.