Work Energy and Power Conservation of Energy Collisions Notes in pdf

PHYSICAL DEFINITION WORK

When the point of application of force moves in the direction of the applied force under its effect then work is said to be done.

MATHEMATICAL DEFINITION OF WORK

Work is defined as the product of force and displacement in the direction of force

W = F × s
If force and displacement are not parallel to each other rather they are inclined at an angle, then in the evaluation of work component of force (F) in the direction of displacement (s) will be considered.

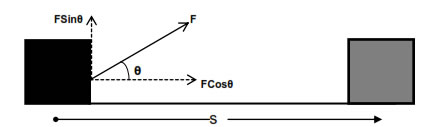
W = (Fcosθ) × s
W = FsCosθ

VECTOR DEFINITION OF WORK

Force and displacement both are vector quantities but their product, work is a scalar quantity, hence work must be scalar product or dot product of force and displacement vector.

W = F . s

WORK DONE BY VARIABLE FORCE

Force varying with displacement In this condition we consider the force to be constant for any elementary displacement and work done in that elementary displacement is evaluated. Total work is obtained by integrating the elementary work from initial to final limits.

 

Force varying with time

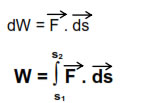
In this condition we consider the force to be constant for any elementary displacement and work done in that elementary displacement is evaluated.

WORK DONE BY VARIABLE FORCE FROM GRAPH

Let force be the function of displacement & its graph be as shown.

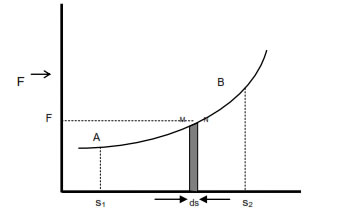
To find work done from s₁ to s₂ we consider two points M & N very close on the graph such that magnitude of force (F) is almost same at both the points. If elementary displacement from M to N is ds, then elementary work done from M to N is.

dW = F.ds
dW = (length x breadth)of strip MNds
dW = Area of strip MNds

Thus work done in any part of the graph is equal to area under that part. Hence total work done from s ₁ to s₂ will be given by the area enclosed under the graph from s₁to s_2.

W = Area (ABS₂ S₁A)

ENERGY

Capacity of doing work by a body is known as energy.
Note - Energy possessed by the body by virtue of any cause is equal to the total work done by thebody when the cause responsible for energy becomes completely extinct.

TYPES OF ENERGIES

There are many types of energies like mechanical energy, electrical, magnetic, nuclear, solar, chemical etc.

MECHANICAL ENERGY

Energy possessed by the body by virtue of which it performs some mechanical work is known as mechanical energy. It is of basically two types-

(i) Kinetic energy

(ii) Potential energy

KINETIC ENERGY

Energy possessed by body due to virtue of its motion is known as the kinetic energy of the body. Kinetic energy possessed by moving body is equal to total work done by the body just before coming out to rest.

Kinetic energy = 1/2 mv²

KINETIC ENERGY IN TERMS OF MOMENTUM

K.E. of body moving with velocity v is

POTENTIAL ENERGY

Energy possessed by the body by virtue of its position or state is known as potential energy. Example:- gravitational potential energy, elastic potential energy, electrostatic potential energy etc.

GRAVITATIONAL POTENTIAL ENERGY

Energy possessed by a body by virtue of its height above surface of earth is known as gravitational potential energy. It is equal to the work done by the body situated at some height in returning back slowly to the surface of earth.

Consider a body of mass m situated at height h above the surface of earth. Force applied by the body in vertically downward direction is

F = mg

Displacement of the body in coming back slowly to the surface of earth is

s = h

Hence work done by the body is

W = FsCosθ

or, W = FsCos0

or, W = mgh

This work was stored in the body in the form of gravitational potential energy due to its position. Therefore

G.P.E = mgh

ELASTIC POTENTIAL ENERGY

Energy possessed by the spring by virtue of compression or expansion against elastic force in the spring is known as elastic potential energy.

Spring

It is a coiled structure made up of elastic material & is capable of applying restoring force & restoring torque when disturbed from its original state. When force (F) is applied at one end of the string, parallel to its length, keeping the other end fixed, then the spring expands (or contracts) & develops a restoring force (F_r) which balances the applied force in equilibrium.

On increasing applied force spring further expands in order to increase restoring force for balancing the applied force. Thus restoring force developed within the spring is directed proportional to the extension produced in the spring.

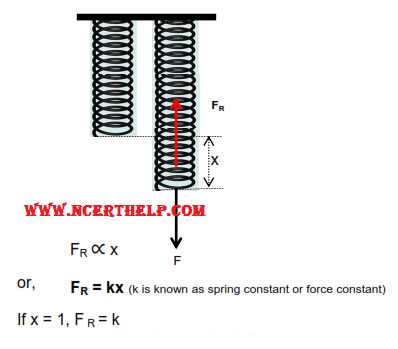
Hence force constant of string may be defined as the restoring force developed within spring when its length is changed by unity.

But in equilibrium, restoring force balances applied force.

F = F_R = k× x

If x = 1, F = 1

Hence force constant of string may also be defined as the force required to change its length by unity in equilibrium.

Mathematical Expression for Elastic Potential Energy  

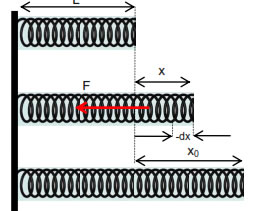
Consider a spring of natural length ‘L’ & spring constant ‘k’ its length is increased by x_o. Elastic potential energy of stretched spring will be equal to total work done by the spring in regaining its original length.

If in the process of regaining its natural length, at any instant extension in the spring was x then force applied by spring is

F = kx

If spring normalizes its length by elementary distance dx opposite to x under this force then work done by spring is

dW = F. (-dx) . Cos0

(force applied by spring F and displacement –dx taken opposite to extension x are in same direction)

dW = -kxdx

dW = -kxdx

Total work done by the spring in regaining its original length is obtained in integrating dW from x₀to 0

WORK ENERGY THEOREM

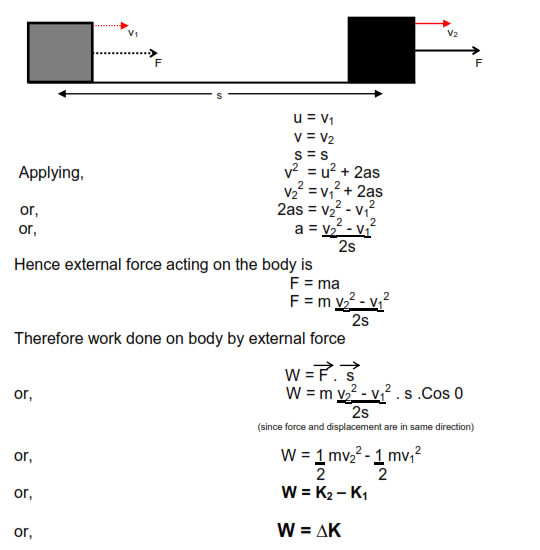
It states that total work done on the body is equal to the change in kinetic energy.(Provided body is confined to move horizontally and no dissipating forces are operating).

Consider a body of man m moving with initial velocity v₁ . After travelling through displacement s its final velocity becomes v₂ under the effect of force F.

PRINCIPLE OF CONSERVATION OF ENERGY

It states that energy can neither be creased neither be destroyed. It can only be converted from one form to another.Consider a body of man m situated at height h & moving with velocity v_o.

CONSERVATIVE FORCE

Forces are said to be conservative in nature if work done against thforces gets conversed in the body in form of potential energy. Example:gravitational forces, elastic forces & all the central forces.

PROPERTIES OF CONSERVATIVE FORCES

1. Work done against these forces is conserved & gets stored in the body in the form of P.E.

2. Work done against these forces is never dissipated by being converted into nonusable forms of energy like heat, light, sound etc.

3. Work done against conservative forces is a state function & not path function i.e. Work done against it, depends only upon initial & final states of body & is independent of the path through which process has been carried out.

4. Work done against conservative forces is zero in a complete cycle.

NON-CONSERVATIVE FORCES

Non conservative forces are the forces, work done against which does not get conserved in the body in the form of potential energy.

PROPERTIES OF NON-CONSERVATIVE FORCES

1. Work done against these forces does not get conserved in the body in the form of P.E.

2. Work done against these forces is always dissipated by being converted into non usable forms of energy like heat, light, sound etc.

3. Work done against non-conservative force is a path function and not a state function.

4. Work done against non-conservative force in a complete cycle is not zero.

POWER

Rate of doing work by a body with respect to time is known as power.

Average Power

It is defined as the ratio of total work done by the body to total time taken

Instantaneous Power

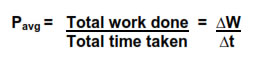
Power developed within the body at any particular instant of time is known as instantaneous power. avg

Or

Average power evaluated for very short duration of time is known as instantaneous power.

EFFICIENCY

It is defined as the ratio of power output to power input.

Or It is defined as the ratio of energy output to energy input.

Or I It is defined as the ratio of work output to work input.

PERCENTAGE EFFICIENCY

Percentage Efficiency = Efficiency x 100

COLLISION

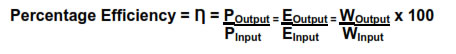
Collision between the two bodies is defined as mutual interaction of the bodies for a short interval of time due to which the energy and the momentum of the interacting bodies change.

Types of Collision

There are basically three types of collisions-

i) Elastic Collision –

That is the collision between perfectly elastic bodies. In this type of collision, since only conservative forces are operating between the interacting bodies, both kinetic energy and momentum of the system remains constant.

ii) Inelastic Collision –

That is the collision between perfectly inelastic or plastic bodies. After collision bodies stick together and move with some common velocity. In this type of collision only momentum is conserved. Kinetic energy is not conserved due to the presence of non-conservative forces between the interacting bodies.

iii) Partially Elastic or Partially Inelastic Collision –

That is the collision between the partially elastic bodies. In this type of collision bodies do separate from each other after collision but due to the involvement of non-conservative inelastic forces kinetic energy of the system is not conserved and only momentum is conserved.

Consider two bodies of masses m₁ and m₂ with their center of masses moving along the same straight line in same direction with initial velocities u and u₂ with m₁ after m₂. Condition necessary for the collision is u₁ > u₂ due to which bodies start approaching towards each other with the velocity of approach u₂-u₁ . Collision starts as soon as the bodies come in contact. Due to its greater velocity and inertia m₁continues to push m ₂in the forward direction whereas m due to its small velocity and inertia pushes m₁ in the backward direction. Due to this pushing force involved between the two colliding bodies they get deformed at the point of contact and a part of their kinetic energy gets consumed in the deformation of the bodies. Also m₁ being pushed opposite to the direction of the motion goes on decreasing its velocity and m being pushed in the direction of motion continues increasing its velocity. This process continues until both the bodies acquire the same common velocity v. Up to this stage there is maximum deformation in the bodies maximum part of their kinetic energy gets consumed in their deformation.

Elastic collision

In case of elastic collision bodies are perfectly elastic. Hence after their maximum deformation they have tendency to regain their original shapes, due to which they start pushing each other. Since m₂ is being pushed in the direction of motion its velocity goes on increasing and m₁ being pushed opposite to the direction of motion its velocity goes on decreasing. Thus condition necessary for separation i.e. v is attained and the bodies get separated with velocity of separation v₂ - v₁ .

In such collision the part of kinetic energy of the bodies which has been consumed in the deformation of the bodies is again returned back to the system when the bodies regain their original shapes. Hence in such collision energy conservation can also be applied along with the momentum conservation. Applying energy conservation.

Hence in perfectly elastic collision between two bodies of same mass, the velocities interchange.ie. If a moving body elastically collides with a similar body at rest. Then the moving body comes at rest and the body at rest starts moving with the velocity of the moving body.

Hence if a huge body elastically collides with a small body then there is almost no change in the velocity of the huge body but if the small body is initially at rest it gets thrown away with twice the velocity of the huge moving body.eg. collision of truck with a drum.

Case 3- If a small body elastically collides with a huge body,

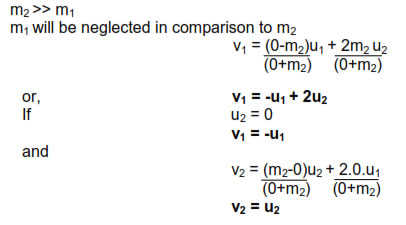
Hence if a small body elastically collides with a huge body at rest then there is almost no change in the velocity of the huge body but if the huge body is initially at rest small body rebounds back with the same speed.eg. collision of a ball with a wall.

Inelastic collision

In case of inelastic collision bodies are perfectly inelastic. Hence after their maximum deformation they have no tendency to regain their original shapes, due to which they continue moving with the same common velocity.

In such collision the part of kinetic energy of the bodies which has been consumed in the deformation of the bodies is permanently consumed in the deformation of the bodies against non-conservative inelastic forces. Hence in such collision energy conservation can-not be applied and only momentum conservation is applied.

Applying momentum conservation

Partially Elastic or Partially Inelastic Collision

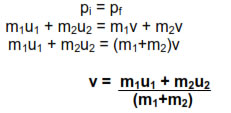
In this case bodies are partially elastic. Hence after their maximum
deformation they have tendency to regain their original shapes but not as much as perfectly elastic bodies. Hence they do separate but their velocity of separation is not as much as in the case of perfectly elastic bodies i.e. their velocity of separation is less than the velocity of approach.
In such collision the part of kinetic energy of the bodies which has
been consumed in the deformation of the bodies is only slightly returned back to the system. Hence in such collision energy conservation can-not be applied and only momentum conservation is applied.

(v₂ -v₁) < (u₁-u₂)

Collision In Two Dimension – Oblique Collision

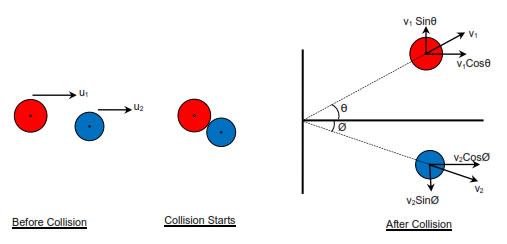
When the centers of mass of two bodies are not along the same straight line, the collision is said to be oblique. In such condition after collision bodies are deflected at some angle with the initial direction. In this type of collision momentum conservation is applied separately along x-axis and y-axis. If the collision is perfectly elastic energy conservation is also applied

e = (v₂-v₁)/(u₁-u₂)

Case-1 For perfectly elastic collision, velocity of separation is equal to velocity of approach, therefore

e = 1

Case-2 For perfectly inelastic collision, velocity of separation is zero, therefore

e = 0

Case-3 For partially elastic or partially inelastic collision, velocity of separation is less than velocity of approach, therefore

e < 1

Ncert Solution for class 6 to 12 download in pdf