
projectile motion examples, example of projectile motion, examples of projectile motion, projectile examples, examples of projectile, which are examples of projectile motion, projectile motion example, projectile motion example problems, physics projectile motion examples, projectile motion with examples, example projectile motion, what is an example of projectile motion, example of projectile, projectile example, example of a projectile, motion in plane, motion in a plane notes, motion in a pla, motion in a plane 11 notes, class 11 physics notes, motion in a plane class 11, motion in a plane class 11 notes, class 11 motion in a plane, note physics, physics notes, motion in a plane, class 11 cphysics chapter 4 notes, 11th standard physics notes, 11th std physics notes, class 11
The quantities which have magnitude only but no direction. For example : mass, length, time, speed , temperature etc.
The quantities which have magnitude as well as direction and obeys vector laws of addition, multiplication etc. For examples : Displacement, velocity, acceleration, force , momentum etc.
(i) Only vectors of same nature can be added.
(ii) The addition of two vector A and B is resultant R
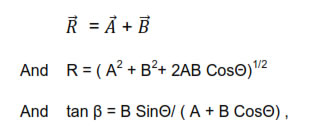
Where Θ is the angle between vector A and vector B, And β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B = B+A
(iv) Vector addition is associative,A+ (B +C ) = (A +B )+C
(v) R is maximum if Θ = 0 and minimum if Θ = 180 + 0 .
(i) Only vector of same nature can be subtracted.
(ii) Subtraction of B from A = vector addition of A and (-B),

Where Θ is the angle between A and B and β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B ≠ B+A
(iv) Vector addition is associative,A+ (B +C ) ≠ (A +B )+C
If A makes an angle Θ with x-axis and Ax and By be the rectangular components of A along X-axis and Y- axis respectively.
Then A= A x + By= y
Here A x =A CosΘ and B y = ASinΘ
The dot product of two vectors A and B, represented by . is a scalar , which is equal to the product of the magnitudes of A and B and the Cosine of the smaller angle between them. If Θ is the smaller angle between A and B, then AB= AB
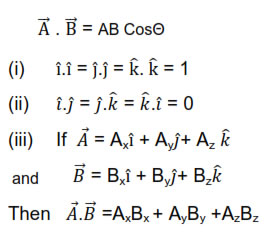
The cross product of two vectors and , represented by x is a vector , which is equal to the product of the magnitudes of A and B and the sine of the smaller angle between them. If Θ is the smaller angle between A and B, then = AB Sinθ

Projectile is the name given to anybody which once thrown in to space with some initial velocity, moves thereafter under the influence of gravity alone without being propelled by any engine or fuel. The path followed by a projectile is called its trajectory.

When a body moves such that it always remains at a fixed distance from a fixed point then its motion is said to be circular motion. The fixed distance is called the radius of the circular path and the fixed point is called the center of the circular path.
When an object follows a circular path at constant speed. The motion of the object is called uniform circular motion.
The magnitude of its acceleration is a c = v2/R.
The direction of a c is always towards the centre of the circle.
Angle swept by the radius vector of a particle moving on a circular path is known as angular displacement of the particle. Example :– angular displacement of the particle from P1 to P2 is θ.
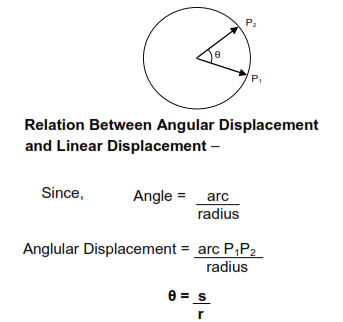
The angular speed is the rate of change of angular distance.
It is related velocity v by V =ω R. The acceleration is ac= ω2R.
If T is the time period of revolution of the object in circular motion and ν is the frequency then we have ω = 2πνV = 2πνR and acceleration a= 4π2 ν 2 R

Angular velocity of a body at some particular instant of time is known as instantaneous angular velocity.
Or
Average angular velocity evaluated for very short duration of time is known as instantaneous angular velocity.

Total time taken by the particle performing uniform circular motion to complete one full circular path is known as time period. In one time period total angle rotated by the particle is 2π and time period is T. Hence angular velocity
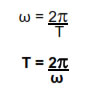
Number of revolutions made by the particle moving on circular path in one second is known as frequency.
f = 1/T = ω/2π
When a body performs uniform circular motion its speed remains constant but velocity continuously changes due to change of direction. Hence a body is continuously accelerated and the acceleration experienced by the body is known as centripetal acceleration (that is the acceleration directed towards the center).
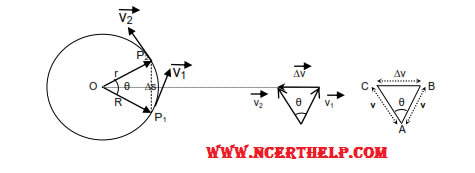
Consider a particle performing uniform circular motion with speed v. When the particle changes its position from P1 to P2. its velocity changes from v1 to v2 due to change of direction. The change in velocity from P1 to p2is ∆v which is directed towards the center of the circular path according to triangle law of subtraction of vectors.
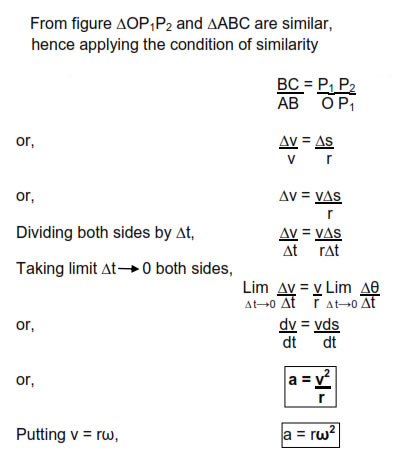
Since the change of velocity is directed towards the center of the circular path, the acceleration responsible for the change in velocity is also directed towards center of circular path and hence it is known as centripetal acceleration.
Centripetal force is the name given to the force that provides inward radial acceleration to a body in circular motion.We should always look for some materia lforce like tension, gravitational force, electrical force, frictionetc. as the centripetal force.
i)Case - 1 Circular motion of a stone tied to a string. Centripetal force is provided by the tension of the string
ii) Case - 2 Circular motion of electron around the nucleus. Centripetal force is provided by the electrostatic force of attraction between thepositively charged nucleus and negatively charged electron
iii) Case - 3 Circular motion of planets around sun or satellites around planet. Centripetal force is provided by the gravitational force of attraction between the planet and sun
iv) Case - 4 Circular motion of vehicles on a horizontal road. Centripetal force is provided by the static frictional force between the road and the tyre of the vehicle.
vi) Case - 6 Circular motion of mud particles sticking to the wheels of the vehicle. Centripetal force is provided by the adhesive force of attraction between the mudparticles and the tyres of the vehicle. At very high speed when adhesive force is unable to provide necessary centripetal force, the mud particles fly off tangentially. In order to prevent the particles from staining our clothes, mud-guards are provided over the wheels of vehicle.
vii) Case - 7 Circular motion of a train on a horizontal track. Centripetal force is provided by the horizontal component of the reaction force applied by the outer track on the inner projection of the outer wheels
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.