Newtons Laws of Motion First Second Third Laws of Inertia

Newton’s 1st law or Law of Inertia

Every body continues to be in its state of rest or of uniform motion until and unless and until it is compelled by an external force to change its state of rest or of uniform motion.

Inertia

The property by virtue of which a body opposes any change in its state of rest or of uniform motion is known as inertia. Greater the mass of the body greater is the inertia. That is mass is the measure of the inertia of the body.
Numerical Application If, F = 0 ; u = constant ( In the absence of external applied force velocity of body remains unchanged.)

Physical Application of inertia or newtons’s first law

1. When a moving bus suddenly stops, passenger’s head gets jerked in the forward direction.
2. When a stationery bus suddenly starts moving passenger’s head gets jerked in the backward direction.
3. On hitting used mattress by a stick, dust particles come out of it.
4. In order to catch a moving bus safely we must run forward in the direction of motion of bus.
5. Whenever it is required to jump off a moving bus, we must always run for a short distance after jumping on road to prevent us from falling in the forward direction.

Newton’s Second law of motion :

It states that the rate of change of momentum of a body is proportional to the applied force and takes place in the direction in which force acts.

Thus F= k dp/dt= k ma

Derivation of second laws of motion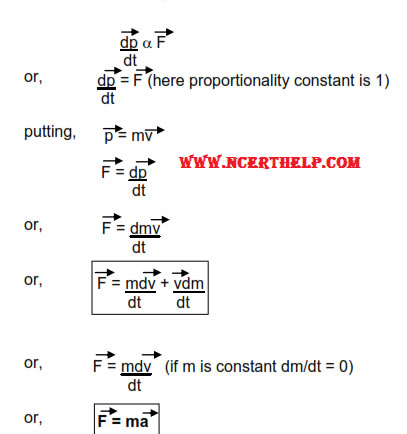

⇒ The second law is consistent with the First law (F=0 implies a=0)
⇒ It is a vector equation
⇒ It is applicable to a particle, and also to a body or a system of particles, provided F the total external force on the system and a is the acceleration of the system as a whole.
⇒ F at a point at a certain instant determines acceleration at the same point at that instant.Acceleration at an instant does not depend on the history of motion’
⇒ Force is not always in the direction of motion .Depending on the situation F may balong V, opposite to v, normal to v, or may make some other angle with v. In everycase it is parallel to acceleration.
⇒ If v=0 at an instant, i.e., if a body is momentarily at rest, it does not mean that force or acceleration are necessarily zero at that instant. For ex: When a ball thrown upward reaches its maximum height, but the force continues to be its weight ‘mg‘ and the acceleration is ‘g’ the acceleration due to gravity.

Note :- Above result is not Newton’s second law rather it is the conditional result obtained from it, under the condition when m = constant.

Numerical Application:

acceleration, a = F _Net / M

Where F _Net is the vector resultant of all the forces acting on the body

Physical Application

i) Case - 1 Body kept on horizontal plane is at rest.
For vertical direction
N = mg(since body is at rest)

ii) Body kept on horizontal plane is accelerating horizontally under single horizontal force.
For vertical direction
N = mg (since body is at rest)
For horizontal direction
F = ma

iii) Body kept on horizontal plane is accelerating horizontally towards right under two horizontal forces. (F1> F2)
For vertical direction
N = mg (since body is at rest)
For horizontal direction F1 - F2= ma

Tension

Tension In A Light String Force applied by any linear object such as string, rope, chain, rod etc. is known as it’s tension. Since string is a highly flexible object so it can only pull the object and can never push. Hence tension of the string always acts away from the body to which it is attached irrespective of the direction.

Physical Application of Tension

i) Flexible wire holding the lamp pulls the lamp in upward direction and pulls the point of suspension in the downward direction.

ii) Rope holding the bucket in the well pulls the bucket in the upward direction and the pulley in the downward direction.

iii) Rope attached between the cattle and the peg pulls the cattle towards the peg and peg towards the cattle.

iv) When a block is pulled by the chain, the chain pulls the block in forward direction and the person holding the chain in reverse direction.
In case of light string, rope, chain, rod etc. tension is same all along their lengths.

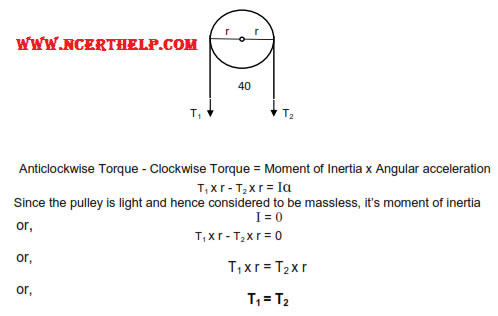
Consider a point P on a light (massless) string. Let tensions on either side of it be T₁ and T₂ respectively and the string be accelerating towards left under these forces. Then for point P2

Since string is considered to be light mass m of point P is zero or, T = 0

Tension of A light Rigid Rod

Force applied by rod is also known as its tension. Since rod is rigid, it cannot bend like string. Hence rod can pull as well as push. Tension of rod can be of pulling as well as pushing nature but one at a time. Tension of a rod attached to the body may be directed towards as well as away from the body.

Physical Application of tension :-

i) Pillars supporting the house pushes the house in the upward direction and pushes the ground in the downward direction.

ii) Wooden bars used in the chair pushes the ground in the downward direction and pushes the seating top in the upward direction.

iii) Parallel bars attached to the ice-cream trolley pushes the trolley in the forward direction and pushes the ice-cream vendor in the backward direction.(when the trolley is being pushed by the vendor)

iv) Rod holding the ceiling fan pulls the fan in the upward direction and pulls the hook attached to the ceiling in the downward direction.

v) Parallel rods attached between the cart and the bull pulls the cart in the forward direction and pulls the bull in the backward direction.

Fixed Pulley

It is a simple machine in the form of a circular disc or rim supported by spokes having groove at its periphery. It is free to rotate about an axis passing through its center and perpendicular to its plane.

Key Point

In case of light pulley, tension in the rope on both the sides of the pulley is same (to be proved in the rotational mechanics)

Newton’ 3rd law or Law of Action and Reaction

Every action is opposed by an equal and opposite reaction.
or
For every action there is an equal and opposite reaction.

F₁₂ is the force on the first body (m₁ ) due to second body (m₂ )

F₂₁ is the force on the second body (m₂) due to first body (m₁)

If F₁₂ is action then F₂₁ reaction and if F₂₁ is action then F₁₂ reaction.

Numerical Application

Force on the first body due to second body (F₁₂ ) is equal and opposite to the force on the second body due to first body (F₂₁ ).

F₂₁ = - F₁₂

Physical Application

i) When we push any block in the forward direction then block pushes us in the backward direction with an equal and opposite force.

ii) Horse pulls the rod attached to the cart in the forward direction and the tension of the rod pulls the cart in the backward direction.

iii) Earth pulls the body on its surface in vertically downward direction and the body pulls the earth with the same force in vertically upward direction.

iv) While walking we push the ground in the backward direction using static frictional force and the ground pushes us in the forward direction using static frictional force.

v) When a person sitting on the horse whips the horse and horse suddenly accelerates, the saddle on the back of the horse pushes the person in the forward direction using static frictional force and the person pushes the saddle in the backward direction using static frictional force.

Note – Normal reaction of the horizontal surface on the body is not the reaction of the weight of the body because weight of the body is the force with which earth attracts the body towards its center, hence its reaction must be the force with which body attracts earth towards it.

Linear Momentum

It is defined as the quantity of motion contained in the body. Mathematically it is given by the product of mass and velocity. It is a vector quantity represented by p.

p = mv

Principle Of Conservation Of Linear Momentum

It states that in the absence of any external applied force total momentum of a system remains conserved. Proof- We know that,

Physical Application of law of conservation of momentum :-

i) Recoil of gun – when bullet is fired in the forward direction gun recoils in the backward direction.

ii) When a person jumps on the boat from the shore of river, boat along with the person on it moves in the forward direction.

iii) When a person on the boat jumps forward on the shore of river, boat starts moving in the backward direction.

iv) In rocket propulsion fuel is ejected out in the downward direction due to which rocket is propelled up in vertically upward direction.

Recoil of gun

Let mass of gun be m_g and that of bullet be m . Initially both are at rest, hence their initial momentum is zero.

p_i = m_gu_g + m_bu_b = 0

Finally when bullet rushes out with velocity v_g, gun recoils with velocity v_b, hence their final momentum is

p_f = m_gv_g + m_b v_b

Since there is no external applied force, from the principal of conservation of linear momentum

p_i = p_f

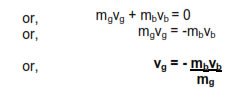
From above expression it must be clear that

1. Gun recoils opposite to the direction of motion of bullet.

2. Greater is the mass of mullet m_b or velocity of bullet v_b greater is the recoil of the gun.

3. Greater is the mass of gun m_g , smaller is the recoil of gun.

Impulse and Impulsive Force

ImpulsiveForce

The force which acts on a body for very short duration of time but is still capable of changing the position, velocity and direction of motion of the body up to large extent is known as impulsive force.

Example -

1. Force applied by foot on hitting a football.

2. Force applied by boxer on a punching bag.

3. Force applied by bat on a ball in hitting it to the boundary.

4. Force applied by a moving truck on a drum.

Note- Although impulsive force acts on a body for a very short duration of time yet its magnitude varies rapidly during that small duration.

Impulse

Impulse received by the body during an impact is defined as the product of average impulsive force and the short time duration for which it acts.

I = F_avg× t

Relation Between Impulse and Linear Momentum

Consider a body being acted upon by an impulsive force, this force changes its magnitude rapidly with the time. At any instant if impulsive force is F then elementary impulse imparted to the body in the elementary time dt is given by

Hence impulse imparted to the body is equal to the change in its momentum.

Graph Between Impulsive Force and Time

With the time on x axis and impulsive force on y axis the graph of thefollowing nature is obtained.

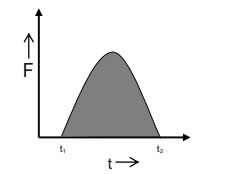
Area enclosed under the impulsive force and time graph from t₁to t₂ gives the impulse imparted to the body from time t₁ to t ₂.

Physical Application of Impulsive Force

i) While catching a ball a player lowers his hand to save himself from getting hurt.

ii) Vehicles are provided with the shock absorbers to avoid jerks.

iii) Buffers are provided between the bogies of the train to avoid jerks.

iv) A person falling on a cemented floor receive more jerk as compared to that falling on a sandy floor.

v) Glass wares are wrapped in a straw or paper before packing.

Equilibrium of Concurrent Forces

If the number of forces act at the same point, they are called concurrent forces. The condition or the given body to be in equilibrium under the number of forces acting on the body is that these forces should produce zero resultant. The resultant of the concurrent forces acting on a body will be zero if they can be represented completely by the sides of a closed polygon taken in order.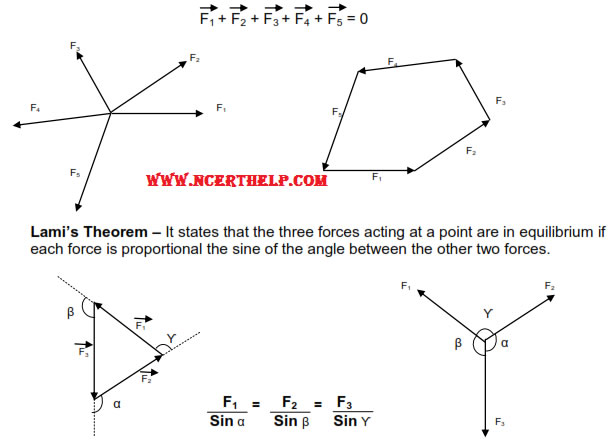

FRICTION

Friction - The property by virtue of which the relative motion between two surfaces in contact is opposed is known as friction.

Frictional Forces - Tangential forces developed between the two surfaces in contact, so as to oppose their relative motion are known as frictional forces or commonly friction.

Types of Frictional Forces

- Frictional forces are of three types :-
1. Static frictional force
2. Kinetic frictional force
3. Rolling frictional force

Static Frictional Force -

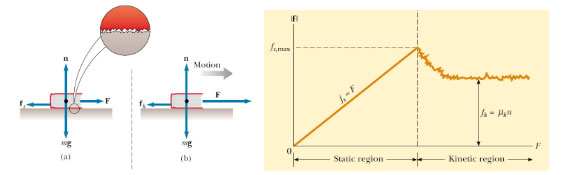
Frictional force acting between the two surfaces in contact which are relatively at rest, so as to oppose their relative motion, when they tend to move relatively under the effect of any external force is known as static frictional force. Static frictional force is a self adjusting force and its value lies between its minimum value up to its maximum value.

Minimum value of static frictional force -

Minimum value of static frictional force is zero in the condition when the bodies are relatively at rest and no external force is acting to move them relatively.
fs(min) = 0

Maximum value of static frictional force -

Maximum value of static frictional force is µsN (where µs is the coefficient of static friction for the given pair of surface and N is the normal reaction acting between the two surfaces in contact) in the condition when the bodies are just about to move relatively under the effect of external applied force.
fs(max) = µsN

Therefore,                                     fs(min) ≤ fs ≤ fs(max)

or,                                                       0 ≤ fs ≤ µsN

Kinetic  Frictional  Force  -  

Frictional  force  acting  between  the  two  surfaces  in contact which are moving relatively, so as to oppose their relative motion, is known as kinetic frictional force. It’s magnitude is almost constant and is equal to µkN where µk is the coefficient of kinetic friction for the given pair of surface and N is the normal reaction acting between the two surfaces in contact. It is always less than maximum value of static frictional force.

fk = µkN Since,

fk < fs(max) = µsN

Therefore, µkN < µsN

or, µk < µs

Limiting Frictional Force –

The maximum value of static frictional force is the maximum frictional force which can act between the two surfaces in contact and hence it is also known as limiting frictional force.

Laws of Limiting Frictional Force –

1. Static friction depends upon the nature of the surfaces in contact.

2. It comes into action only when any external force is applied to move the two bodies relatively, with their surfaces in contact.

3. Static friction opposes the impending motion.

4. It is a self adjusting force.

5. The limiting frictional force is independent of the area of contact between the two surfaces.

Cause of Friction

Old View -

The surfaces which appear to be smooth as seen through our naked eyes are actually rough at the microscopic level. During contact, the projections of one surface penetrate into the depressions of other and vice versa. Due to which the two surfaces in contact form a saw tooth joint opposing their relative motion. When external force is applied so as to move them relatively this joint opposes their relative motion. As we go on increasing the external applied force the opposition of saw tooth joint also goes on increasing up to the maximum value known as limiting frictional force (µ_s N) after which the joint suddenly breaks and the surfaces start moving relatively. After this the opposition offered by the saw tooth joint slightly decreases and comes to rest at almost constant value (µ_kN)

Modern View –

According to modern theory the cause of friction is the atomic and molecular forces of attraction between the two surfaces at their actual point of contact. When any body comes in contact with any other body then due to their roughness at the microscopic level they come in actual contact at several points. At these points the atoms and molecules come very close to each other and intermolecular force of attraction start acting between them which opposes their relative motion.

Contact Force -

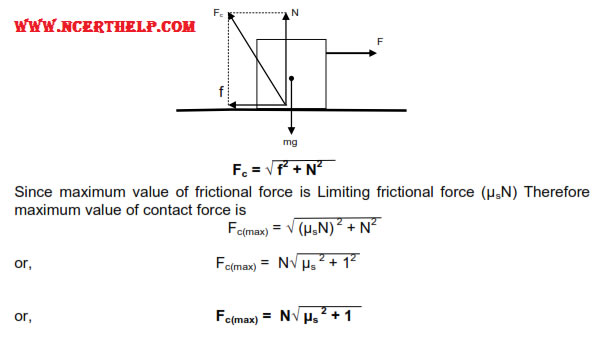
The forces acting between the two bodies due to the mutual contact of their surfaces are known as contact forces. The resultant of all the contact forces acting between the bodies is known as resultant contact force. Example friction (f) and normal reaction (N) are contact forces and their resultant (F_c) is the resultant is the resultant contact force.

Rolling Frictional Force -

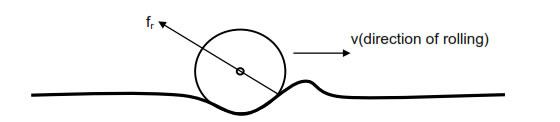
Frictional force which opposes the rolling of bodies (like cylinder, sphere, ring etc.) over any surface is called rolling frictional force. Rolling frictional force acting between any rolling body and the surface is almost constant and is given by µ_r N. Where µ is coefficient of rolling friction and N is the normal reaction between the rolling body and the surface. r

Cause of Rolling Friction –

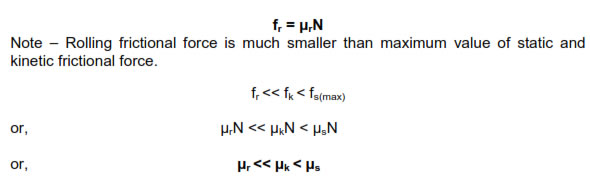
When any body rolls over any surface it causes a little depression and a small hump is created just ahead of it. The hump offers resistance to the motion of the rolling body, this resistance is rolling frictional force. Due to this reason only, hard surfaces like cemented floor offers less resistance as compared to soft sandy floor because hump created on a hard floor is much smaller as compared to the soft floor.

Need to Convert Kinetic Friction into Rolling Friction –

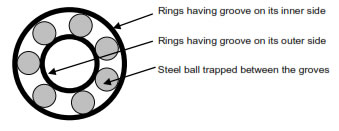
Of all the frictional forces rolling frictional force is minimum. Hence in order to avoid the wear and tear of machinery it is required to convert kinetic frictional force into rolling frictional force and for this reason we make the use of ball-bearings.

Friction:

A Necessary Evil –

Although frictional force is a non-conservative force and causes lots of wastage of energy in the form of heat yet it is very useful to us in many ways. That is why it is considered as a necessary evil.

Advantages of Friction -

i) Friction is necessary in walking. Without friction it would have been impossible for us to walk.

ii) Friction is necessary for the movement of vehicles on the road. It is the static frictional force which makes the acceleration and retardation of vehicles possible on the road.

iii) Friction is helpful in tying knots in the ropes and strings.

iv) We are able to hold anything with our hands by the help of friction only.

Disadvantages of Friction -

i) Friction causes wear and tear in the machinery parts.

ii) Kinetic friction wastes energy in the form of heat, light and sound.

iii) A part of fuel energy is consumed in overcoming the friction operating within the various parts of machinery.

Methods to Reduce Friction –

i) By polishing – Polishing makes the surface smooth by filling the space between the depressions and projections present in the surface of the bodies at microscopic level and there by reduces friction.

ii) By proper selection of material – Since friction depends upon the nature of material used hence it can be largely reduced by proper selection of materials.

iii) By lubricating – When oil or grease is placed between the two surfaces in contact, it prevents the surface from coming in actual contact with each other. This converts solid friction into liquid friction which is very small.

Banking of Roads

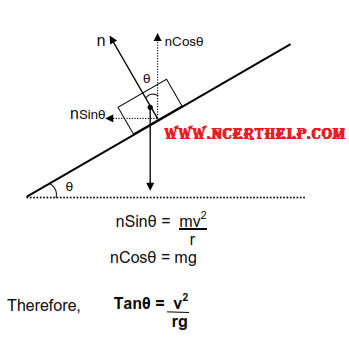
In case of horizontal road necessary centripetal force mv²/r is provided by static frictional force. When heavy vehicles move with high speed on a sharp turn (small radius) then all the factors contribute to huge centripetal force which if provided by the static frictional force may result in the fatal accident. To prevent this roads are banked by lifting their outer edge.Due to this, normal reaction of road on the vehicle gets tilted inwards such that it’s vertical component balances the weight of the body and the horizontal component provides the necessary centripetal force.

 

Ncert Solution for class 6 to 12 download in pdf