ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS

• The phenomenon of production of induced emf in a conductor when electric flux linked with that changes is called electromagnetic induction.

• Magnetic flux through a surface of area A placed in a uniform magnetic field B is defined as  Cosθ where θ is the angle between B and A.

• Magnetic flux is a scalar quantity and its SI unit is weber (Wb).

• Faraday’s laws of induction:

First Law: When magnetic flux linked with the conductor changes, induced emf produces across it. Second Law:

The magnitude of the induced e.m.f in a circuit is equal to the rate of change of magnitude flux linked with that circuit 

• Lenz law:

The direction of induced current or the polarity of the induced e.m.f is in such a way that it opposes the cause that produces it. (The negative sign in Faraday’s law indicates this fact.) Lenz law obeys the principle of energy conservation.

• The induced current in a closed loop can be produced by changing the
(i) magnitude of B
(ii) area A of the loop
(iii) its orientation in magnetic field.

• The direction of induced current is obtained from Fleming’s right hand rule.

• When a metal rod of length l is placed normal to a uniform magnetic field B and moved with a velocity v perpendicular to the field, the induced e.m.f is called motional e.m.f. It produces across the ends of the rod. ε = Blv.If ‘R’ is the resistance of the metal rod, the induced current is given by I=Blv/R, the force acting on the conductor in the presence of magnetic field (due to drift of charge) is given by F =B²l²v / R. The power required to move the conductor with a constant speed is given by P= B²l²v²/R.

• The induced currents produced on the surface of a thick conductor when magnetic flux linked with that changes are called eddy currents.

• The phenomenon of production of induced emf in a coil itself when electric current passing through that changes is called self induction. Self Inductance is the ratio of the flux linkage to current. = 

• When a current in a coil changes it induces a back e.m.f in the same coil. The self induced e.m.f is given by ε = where L is the self-inductance of the coil. It is a measure of inertia of the coil against the change of current through it. Its S.I unit is henry (H).

• The inductance is said to be one Henry when an emf of one volt induces in a coil for unit rate of change of electric current through it.

• The changing current in a coil can induce an e.m.f in a nearby coil. This relation, ε = shows that Mutual inductance of coil 1 with respect to coil 2 (M₁₂) is due to change of current in coil 2. (M₁₂ =M₂₁).

• The self-inductance of a long solenoid is given by L = μ₀n²Al where A is the area of cross-section of the solenoid, l is its length and n is the number of turns per unit length. 

• The mutual inductance of two co-axial coils is given by M₁₂ = M₂₁ = μM⁰ n₁n₂A_l where n1& n2 are the number of turns per unit length of coils 1 & 2. A is the area of cross-section and l is the length of the solenoids.

• Energy stored in an inductor in the form of magnetic field is and Magnetic energy density

• The electric current whose magnitude changes continuously and direction changes periodically is called alternating current (AC). I = Io Sin ωt. • The root mean square value of a.c. may be defined as that value of steady current which would generate the same amount of heat in a given resistance in a given time as is done by the a.c. when passed through the same resistance during the same time. Irms = I_o/√2 = 0.707i0 . Similarly, vrms = v_o/√2 = 0.707v_o. 

• The rotating vectors which represent the varying quantities are called phasors. The diagram in which the AC voltage and AC currents are represented as phasors is called phasor diagram.

• The opposition offered by resistor is called resistance (R). The non-resistive opposition offered by a device is called reactance (X). The combination of reactance and resistance is called impedance (Z). 

• An alternating voltage ε=ε₀Sinωt, applied to a resistor R drives a current I = I₀Sinωt in the resistor, I₀ = ε₀ /R where ε₀& I₀ are the peak values of voltage and current. (also represented by V_m & I_m)

• For an AC e_mf ε = ε_m Sin ωt applied to a resistor, current and voltage are in phase.

• In case of an a.c. circuit having pure inductance current lags behind e.m.f by a phase angle 90°. ε = εm Sin ωt and i = i_m Sin (ωt-π/2). I_m = ε_m/X_L; X_L = ωL is called inductive reactance. 

• In case of an a.c. circuit having pure capacitance, current leads e._m.f by a phase angle of 90°. ε = ε_mSinωt and I= I_mSin(ωt+π/2) where I_m = ε_m/X_C and X_C = 1/ωC is called capacitive reactance.

• In case of an a.c. circuit having R, L and C, the total or effective resistance of the circuit is called impedance (Z). 

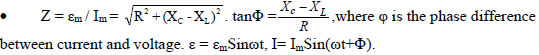
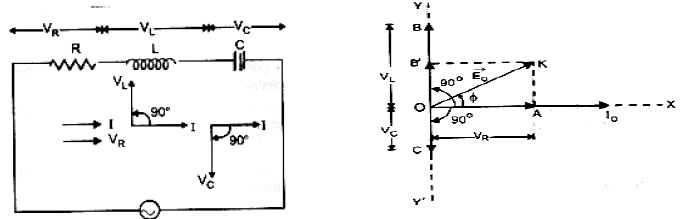
• Average power loss over a complete cycle in an LCR circuit is P = ε_rmsI_rmsCosΦ

• In a purely resistive circuit Φ = 0; P = V_RMSI_RMS.
• In a purely inductive circuit Φ = π/2; P = 0.
• In a purely capacitive circuit Φ = π/2; P = 0.

• The electric current in an AC circuit is said to be wattless current when average power dissipated or consumed is zero.

• In an LCR circuit, the circuit admits maximum current if X_C = X_L, so that Z = R and resonant frequency w_r 

• The device which converts mechanical energy in to AC electrical energy by virtue of electromagnetic induction is called AC Generator.

• Rotation of rectangular coil in a magnetic field causes change in flux (Φ = NBACosωt). Change in flux induces e.m.f in the coil which is given by ε= -dΦ/dt = NBAωSinωt. ε = ε₀Sinωt. Current induced in the coil I = ε/R = ε₀Sinωt/R = I₀Sinωt

• The device which converts an AC voltage of one value to another is called Transformer. For an ideal transformer,• In an ideal transformer, εPIP = εSIS. i.e

• If N_S>N_P; ε_S>ε_P& I_S< I_P – step up. If N_P>N_S; εP>ε_S & I_PI_S – step down.

• Losses in transformer: Copper losses; Iron losses, Flux losses; Hysteresis losses; Humming losses.

• When a charged capacitor is allowed to discharge through an inductor, electrical oscillations of constant amplitude and frequency are produced, which is called LC oscillations. The charge on capacitor q satisfies the equation of SHM 

•

Ncert Solution for class 6 to 12 download in pdf