Class 12 Maths NCERT Solutions For Chapter 13 Probability

Chapter 13 Probability

Download NCERT Solutions for Class 12 Mathematics

(Link of Pdf file is given below at the end of the Questions List)

In this pdf file you can see answers of following Questions

Question 7. Two coins are tossed once, where (i) E : tail appears on one coin, F : one coin shows head (ii) E : no tail appears, F : no head appears

Question 8. A die is thrown three times, E : 4 appears on the third toss, F : 6 and 5 appears respectively on first two tosses

Question 9. Mother, father and son line up at random for a family picture E : son on one end, F : father in middle

Question 10. A black and a red dice are rolled.
(a) Find the conditional probability of obtaining a sum greater than 9, given that the black die resulted in a 5 .
(b) Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Question 11. A fair die is rolled. Consider events E = {1,3,5}, F = {2,3} and G = {2,3,4,5} Find
(i) P(E|F) and P(F|E)
(ii) P(E|G) and P(G|E)
(iii) P((E ∪ F)|G) and P ((E ∩ F)|G)

Question 12. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that (i) the youngest is a girl, (ii) at least one is a girl?

Question 13. An instructor has a question bank consisting of 300 easy True / False questions, 200 difficult True / False questions, 500 easy multiple choice questions and 400 difficult multiple choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple choice question?

Question 14. Given that the two numbers appearing on throwing two dice are different. Find the probability of the event ‘the sum of numbers on the dice is 4’.

Question 15. Consider the experiment of throwing a die, if a multiple of 3 comes up, throw the die again and if any other number comes, toss a coin. Find the conditional probability of the event ‘the coin shows a tail’, given that ‘at least one die shows a 3’. In each of the Exercises 16 and 17 choose the correct answer:

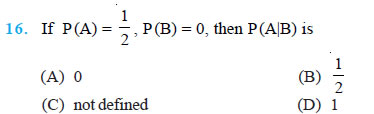
Question 17. If A and B are events such that P(A|B) = P(B|A), then (
A) A ⊂ B but A ≠ B
(B) A = B
(C) A ∩ B = φ
(D) P(A) = P(B)

Question 2. Two cards are drawn at random and without replacement from a pack of 52 playing cards. Find the probability that both the cards are black.

Question 3. A box of oranges is inspected by examining three randomly selected oranges drawn without replacement. If all the three oranges are good, the box is approved for sale, otherwise, it is rejected. Find the probability that a box containing 15 oranges out of which 12 are good and 3 are bad ones will be approved for sale.

Question 4. A fair coin and an unbiased die are tossed. Let A be the event ‘head appears on the coin’ and B be the event ‘3 on the die’. Check whether A and B are independent events or not.

Question 5. A die marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let A be the event, ‘the number is even,’ and B be the event, ‘the number is red’. Are A and B independent?

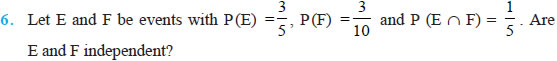
Question 12. A die is tossed thrice. Find the probability of getting an odd number at least once.

Question 13. Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls. Find the probability that
(i) both balls are red.
(ii) first ball is black and second is red.
(iii) one of them is black and other is red.

Question 14. Probability of solving specific problem independently by A and B are 1 2 and 1 3 respectively. If both try to solve the problem independently, find the probability that (i) the problem is solved (ii) exactly one of them solves the problem.

Question 15. One card is drawn at random from a well shuffled deck of 52 cards. In which of the following cases are the events E and F independent ?
(i) E : ‘the card drawn is a spade’ F : ‘the card drawn is an ace’
(ii) E : ‘the card drawn is black’ F : ‘the card drawn is a king’
(iii) E : ‘the card drawn is a king or queen’ F : ‘the card drawn is a queen or jack’.

Question 16. In a hostel, 60% of the students read Hindi news paper, 40% read English news paper and 20% read both Hindi and English news papers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English news papers.
(b) If she reads Hindi news paper, find the probability that she reads English news paper.
(c) If she reads English news paper, find the probability that she reads Hindi news paper. Choose the correct answer in Exercises 17 and 18.

Question 17. The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
(A) 0
(B) 1 3
(C) 1 12
(D) 1 36

Question 18. Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P(A′B′) = [1 – P(A)] [1 – P(B)]
(C) P(A) = P(B)
(D) P(A) + P(B) = 1

Question 16. In a hostel, 60% of the students read Hindi news paper, 40% read English news paper and 20% read both Hindi and English news papers. A student is selected at random.
(a) Find the probability that she reads neither Hindi nor English news papers.
(b) If she reads Hindi news paper, find the probability that she reads English news paper.
(c) If she reads English news paper, find the probability that she reads Hindi news paper. Choose the correct answer in Exercises 17 and 18.

Question 17. The probability of obtaining an even prime number on each die, when a pair of dice is rolled is
(A) 0
(B) 1 3
(C) 1 12
(D) 1 36

Question 18. Two events A and B will be independent, if
(A) A and B are mutually exclusive
(B) P(A′B′) = [1 – P(A)] [1 – P (B)]
(C) P(A) = P(B)
(D) P(A) + P(B) = 1

EXERCISE 13.3

Question 1. An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a ball is drawn at random. What is the probability that the second ball is red?

Question 2. A bag contains 4 red and 4 black balls, another bag contains 2 red and 6 black balls. One of the two bags is selected at random and a ball is drawn from the bag which is found to be red. Find the probability that the ball is drawn from the first bag.

Question 3. Of the students in a college, it is known that 60% reside in hostel and 40% are day scholars (not residing in hostel). Previous year results report that 30% of all students who reside in hostel attain A grade and 20% of day scholars attain A grade in their annual examination. At the end of the year, one student is chosen at random from the college and he has an A grade, what is the probability that the student is a hostlier?

Question 4. In answering a question on a multiple choice test, a student either knows the answer or guesses. Let 3 4 be the probability that he knows the answer and 1 4 be the probability that he guesses. Assuming that a student who guesses at the answer will be correct with probability 1 4 . What is the probability that the student knows the answer given that he answered it correctly?

Question 5. A laboratory blood test is 99% effective in detecting a certain disease when it is in fact, present. However, the test also yields a false positive result for 0.5% of the healthy person tested (i.e. if a healthy person is tested, then, with probability 0.005, the test will imply he has the disease). If 0.1 percent of the population actually has the disease, what is the probability that a person has the disease given that his test result is positive ?

Question 6. There are three coins. One is a two headed coin (having head on both faces), another is a biased coin that comes up heads 75% of the time and third is an unbiased coin. One of the three coins is chosen at random and tossed, it shows heads, what is the probability that it was the two headed coin ?

Question 7. An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?

Question 8. A factory has two machines A and B. Past record shows that machine A produced 60% of the items of output and machine B produced 40% of the items. Further, 2% of the items produced by machine A and 1% produced by machine B were defective. All the items are put into one stockpile and then one item is chosen at random from this and is found to be defective. What is the probability that it was produced by machine B?

Question 9. Two groups are competing for the position on the Board of directors of a corporation. The probabilities that the first and the second groups will win are 0.6 and 0.4 respectively. Further, if the first group wins, the probability of introducing a new product is 0.7 and the corresponding probability is 0.3 if the second group wins. Find the probability that the new product introduced was by the second group.

Question 10. Suppose a girl throws a die. If she gets a 5 or 6, she tosses a coin three times and notes the number of heads. If she gets 1, 2, 3 or 4, she tosses a coin once and notes whether a head or tail is obtained. If she obtained exactly one head, what is the probability that she threw 1, 2, 3 or 4 with the die?

Question 11. A manufacturer has three machine operators A, B and C. The first operator A produces 1% defective items, where as the other two operators B and C produce 5% and 7% defective items respectively. A is on the job for 50% of the time, B is on the job for 30% of the time and C is on the job for 20% of the time. A defective item is produced, what is the probability that it was produced by A?

Question 12. A card from a pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of the lost card being a diamond.

Question 13. Probability that A speaks truth is 4 5 . A coin is tossed. A reports that a head appears. The probability that actually there was head is
(A) 4 5
(B) 1 2
(C) 1 5
(D) 2 5

Question 14. If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is correct?
(A) P(A| B) P(B) P(A) =
(B) P(A|B) < P(A)
(C) P(A|B) ≥ P(A)
(D) None of these

EXERCISE 13.4

Question 1. State which of the following are not the probability distributions of a random variable. Give reasons for your answer.

Question 2. An urn contains 5 red and 2 black balls. Two balls are randomly drawn. Let X represent the number of black balls. What are the possible values of X? Is X a random variable ?

Question 3. Let X represent the difference between the number of heads and the number of tails obtained when a coin is tossed 6 times. What are possible values of X?

Question 4. Find the probability distribution of (i) number of heads in two tosses of a coin. (ii) number of tails in the simultaneous tosses of three coins. (iii) number of heads in four tosses of a coin.

Question 5. Find the probability distribution of the number of successes in two tosses of a die, where a success is defined as (i) number greater than 4 (ii) six appears on at least one die.

Question 6. From a lot of 30 bulbs which include 6 defectives, a sample of 4 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs.

Question 7. A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.

Question 8. A random variable X has the following probability distribution :

Question 9.Determine
(i) k
(ii) P(X < 3)
(iii) P(X > 6)
(iv) P(0 < X < 3)

EXERCISE 13.5

Question 1. A die is thrown 6 times. If ‘getting an odd number’ is a success, what is the probability of (i) 5 successes? (ii) at least 5 successes? (iii) at most 5 successes?

Question 2. A pair of dice is thrown 4 times. If getting a doublet is considered a success, find the probability of two successes.

Question 3. There are 5% defective items in a large bulk of items. What is the probability that a sample of 10 items will include not more than one defective item?

Question 4. Five cards are drawn successively with replacement from a well-shuffled deck of 52 cards. What is the probability that (i) all the five cards are spades? (ii) only 3 cards are spades? (iii) none is a spade?

Question 5. The probability that a bulb produced by a factory will fuse after 150 days of use is 0.05. Find the probability that out of 5 such bulbs (i) none (ii) not more than one (iii) more than one (iv) at least one will fuse after 150 days of use.

Question 6. A bag consists of 10 balls each marked with one of the digits 0 to 9. If four balls are drawn successively with replacement from the bag, what is the probability that none is marked with the digit 0?

Question 7. In an examination, 20 questions of true-false type are asked. Suppose a student tosses a fair coin to determine his answer to each question. If the coin falls heads, he answers ’true’; if it falls tails, he answers ’false’. Find the probability that he answers at least 12 questions correctly.

Question 8. Suppose X has a binomial distribution B 6, 1 2 . Show that X = 3 is the most likely outcome. (Hint : P(X = 3) is the maximum among all P(xi), xi = 0,1,2,3,4,5,6)

Question 9. On a multiple choice examination with three possible answers for each of the five questions, what is the probability that a candidate would get four or more correct answers just by guessing ?

Question 10. A person buys a lottery ticket in 50 lotteries, in each of which his chance of winning a prize is 1 100 . What is the probability that he will win a prize
(a) at least once
(b) exactly once
(c) at least twice?

Question 11. Find the probability of getting 5 exactly twice in 7 throws of a die.

Question 12. Find the probability of throwing at most 2 sixes in 6 throws of a single die.

Question 13. It is known that 10% of certain articles manufactured are defective. What is the probability that in a random sample of 12 such articles, 9 are defective? In each of the following, choose the correct answer:

Question 14. In a box containing 100 bulbs, 10 are defective. The probability that out of a sample of 5 bulbs, none is defective is

Miscellaneous Exercise on Chapter 13

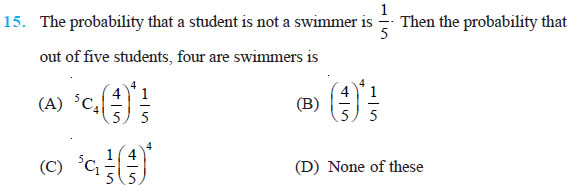
Question 1. A and B are two events such that P (A) ≠ 0. Find P(B|A), if (i) A is a subset of B (ii) A ∩ B = φ

Question 2. A couple has two children, (i) Find the probability that both children are males, if it is known that at least one of the children is male. (ii) Find the probability that both children are females, if it is known that the elder child is a female.

Question 3. Suppose that 5% of men and 0.25% of women have grey hair. A grey haired person is selected at random. What is the probability of this person being male? Assume that there are equal number of males and females.

Question 4. Suppose that 90% of people are right-handed. What is the probability that at most 6 of a random sample of 10 people are right-handed?

Question 5. An urn contains 25 balls of which 10 balls bear a mark ’X’ and the remaining 15 bear a mark ’Y’. A ball is drawn at random from the urn, its mark is noted down and it is replaced. If 6 balls are drawn in this way, find the probability that
(i) all will bear ’X’ mark.
(ii) not more than 2 will bear ’Y’ mark.
(iii) at least one ball will bear ’Y’ mark.
(iv) the number of balls with ’X’ mark and ’Y’ mark will be equal.

Question 6. In a hurdle race, a player has to cross 10 hurdles. The probability that he will clear each hurdle is 5 6 . What is the probability that he will knock down fewer than 2 hurdles?

Question 7. A die is thrown again and again until three sixes are obtained. Find the probability of obtaining the third six in the sixth throw of the die.

Question 8. If a leap year is selected at random, what is the chance that it will contain 53 tuesdays?

Question 9. An experiment succeeds twice as often as it fails. Find the probability that in the next six trials, there will be atleast 4 successes.

Question 10. How many times must a man toss a fair coin so that the probability of having at least one head is more than 90%?

Question 11. In a game, a man wins a rupee for a six and loses a rupee for any other number when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a six. Find the expected value of the amount he wins / loses.

Question 12. Suppose we have four boxes A,B,C and D containing coloured marbles as given below: One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A?, box B?, box C?

Question 13. Assume that the chances of a patient having a heart attack is 40%. It is also assumed that a meditation and yoga course reduce the risk of heart attack by 30% and prescription of certain drug reduces its chances by 25%. At a time a patient can choose any one of the two options with equal probabilities. It is given that after going through one of the two options the patient selected at random suffers a heart attack. Find the probability that the patient followed a course of meditation and yoga?

Question 14. If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability 1 2 ).

Question 15. An electronic assembly consists of two subsystems, say, A and B. From previous testing procedures, the following probabilities are assumed to be known: P(A fails) = 0.2 P(B fails alone) = 0.15 P(A and B fail) = 0.15 Evaluate the following probabilities (i) P(A fails|B has failed) (ii) P(A fails alone)

Question 16. Bag I contains 3 red and 4 black balls and Bag II contains 4 red and 5 black balls. One ball is transferred from Bag I to Bag II and then a ball is drawn from Bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black. Choose the correct answer in each of the following:

Question 17. If A and B are two events such that P(A) ≠ 0 and P(B | A) = 1, then
(A) A ⊂ B
(B) B ⊂ A
(C) B = φ
(D) A = φ

Question 18. If P(A|B) > P(A), then which of the following is correct :
(A) P(B|A) < P
(B) (B) P(A ∩ B) < P(A) . P(B)
(C) P(B|A) > P(B)
(D) P(B|A) = P(B)

Question 19. If A and B are any two events such that P(A) + P(B) – P(A and B) = P(A), then
(A) P(B|A) = 1
(B) P(A|B) = 1
(C) P(B|A) = 0
(D) P(A|B) = 0

Click Here to Download NCERT Solutions for class 12 Mathematics Chapter 13

Please Wait pdf file is loading (कृपया इंतजार करें pdf file लोड हो रही है)...
Loading speed will depend up on your download speed. Pdf file के लोड होने में लगा समय आपकी डाउनलोड स्पीड पर निर्भर करेगा

Download pdf file links for Probability Class 12 NCERT Solutions

Ncert Solution for class 6 to 12 download in pdf

Follow Us On

Facebook

Twitter

Youtube

Linkdin