
trigonometric notes for class 11 chapter 3 download pdf, trigonometric functions 11 notes, class 11 maths notes, trigonometric functions class 11, trigonometric functions class 11 notes, class 11 trigonometric functions, note maths, maths notes, trigonometric functions, class 11 cmaths chapter 3 notes, 11th standard maths notes, 11th std maths notes, class 11 maths notes chapter 3, trigonometric functions chapter class 11 notes
When a ray OA starting from its initial position OA rotates about its end point 0 and takes the final position OB, we say that angle
AOB (written as ∠ AOB) has been formed. The amount of rotation from the initial side to the terminal side is Called the measure of the angle.
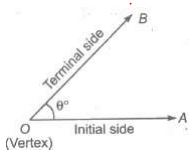
An angle formed by a rotating ray is said to be positive or negative depending on whether it moves in an anti-clockwise or a clockwise direction, respectively.
There are three system for measuring angles,
1. Sexagesimal System/Degree Measure (English System)
In this system, a right angle is divided into 90 equal parts, called degrees. The symbol 1° is used to denote one degree. Each degree is divided into 60 equal parts, called minutes and one minute is divided into 60 equal parts, called seconds. Symbols 1′ and 1″ are used to denote one minute and one second, respectively.
i.e., 1 right angle = 90°
1° = 60′
1′ = 60″
2. Centesimal System (French System)
In this system, a right angle is divided into 100 equal parts, called ‘grades’. Each grade is subdivided into 100 min and each minute is divided into 100 s.
i.e., 1 right angle = 100 grades = 100g
1g = 100′
1′ = 100″
3. Circular System (Radian System) In this system, angle is measured in radian.
A radian is the angle subtended at the centre of a circle by an arc, whose length is equal to the radius of the circle.
The number of radians in an angle subtended by an arc of circle at the centre is equal to arc/radius.
(i) π radian = 180° or 1 radian (180°/π)= 57°16’22” where, π = 22/7 = 3.14159
(ii) 1° = (π/180) rad = 0.01746 rad
(iii) If D is the number of degrees, R is the number of radians and G is the number of grades in an angle θ, then
![]()
(iv) θ = l/r where θ = angle subtended by arc of length / at the centre of the circle, r = radius of the circle.
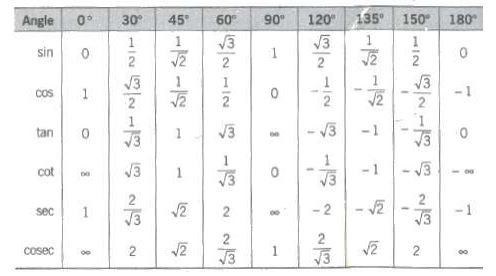
Relation between different sides and angles of a right angled triangle are called trigonometric ratios or T-ratios

Let X’OX and YOY’ be the coordinate axes. Taking 0 as the centre and a unit radius, draw a circle, cutting the coordinate axes at A,B, A’ and B’, as shown in the figure.
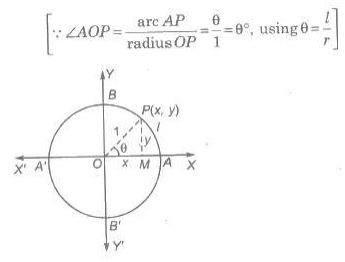
Now, the six circular functions may be defined as under
(i) cos θ = x
(ii) sin θ = y
(iii) sec θ = 1/x, x ≠ 0
(iv) cosec θ = 1/y, y ≠ 0
(v) tan θ = y/x, x ≠ 0
(vi) cot θ = x/y, y ≠ 0

sin θ|≤ 1, |cos θ| ≤ 1, |sec θ| ≥ 1, |Cosec θ| ≥ 1 for all values of 0, for which the functions are defined.
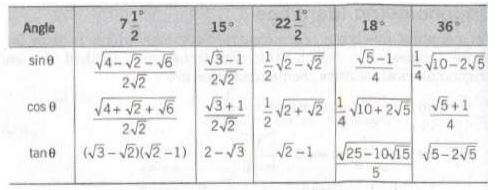
An equation involving trigonometric functions which is true for all those angles for which the functions are defined is called trigonometrical identity. Some identities are
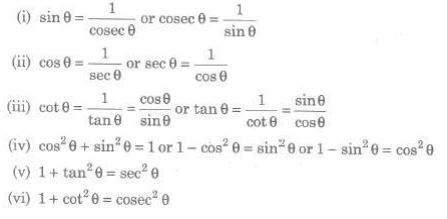
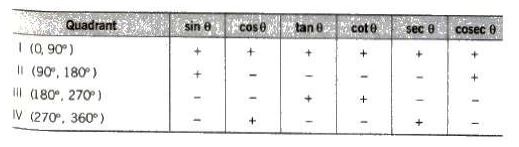
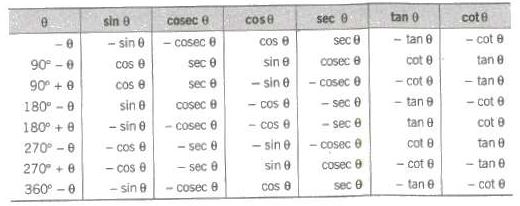
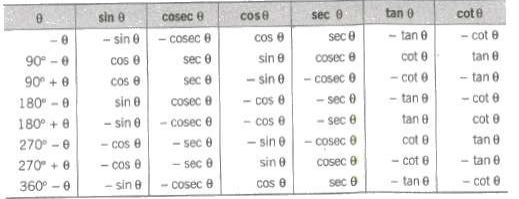
Two angles are said to be allied when their sum or difference is either zero or a multiple of 90°.
The angles — θ, 90° ± θ, 180° ± θ, 270° + θ, 360° —θ etc., are angles allied to the angle θ, if θ is measured in degrees.
A function f(x) is said to be periodic, if there exists a real number T> 0 such that f(x + T)= f(x) for all x. T is called the period of the function, all trigonometric functions are periodic.
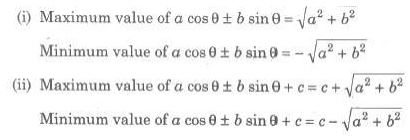
The algebraic sum of two or more angles are generally called compound angles and the angles are known as the constituent angle. Some standard formulas of compound angles have been given below.
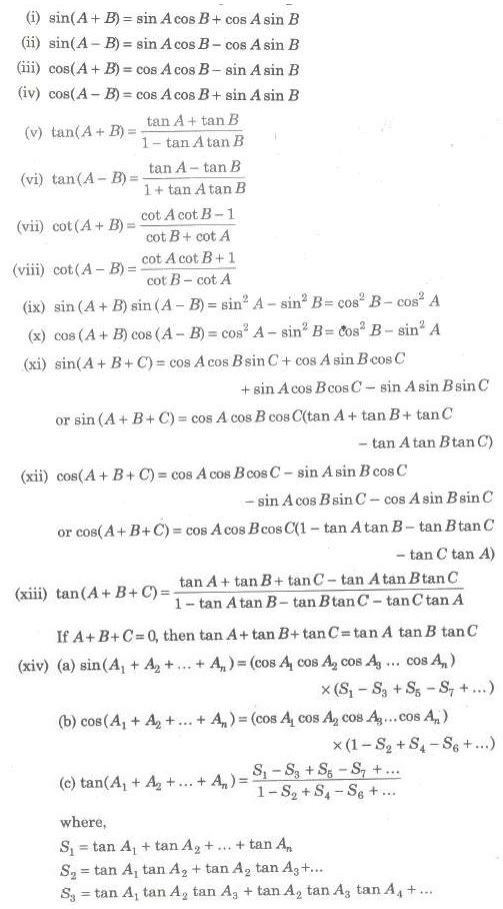
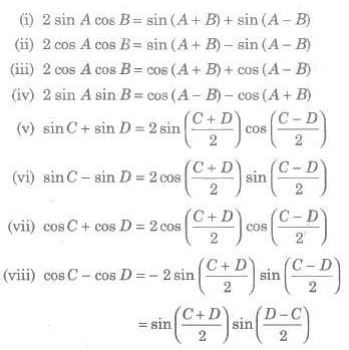
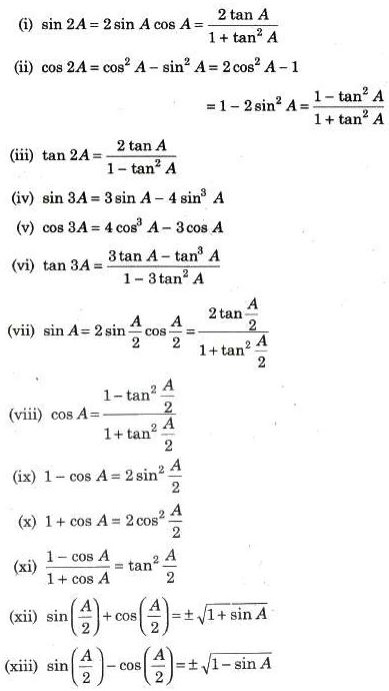


Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.