Application of Integrals Class 12 Notes For Maths Chapter 8

NCERT Notes for Class 12 Mathematics
Chapter 8: Application of Integrals

Let f(x) be a function defined on the interval [a, b] and F(x) be its anti-derivative. Then,

The above is called the second fundamental theorem of calculus.

is defined as the definite integral of f(x) from x = a to x = b. The numbers and b are called limits of integration. We write

Evaluation of Definite Integrals by Substitution

Consider a definite integral of the following form

Step 1 Substitute g(x) = t

⇒ g ‘(x) dx = dt

Step 2 Find the limits of integration in new system of variable i.e.. the lower limit is g(a) and the upper limit is g(b) and the g(b) integral is now

Step 3 Evaluate the integral, so obtained by usual method.

Properties of Definite Integral

13. Leibnitz Rule for Differentiation Under Integral Sign

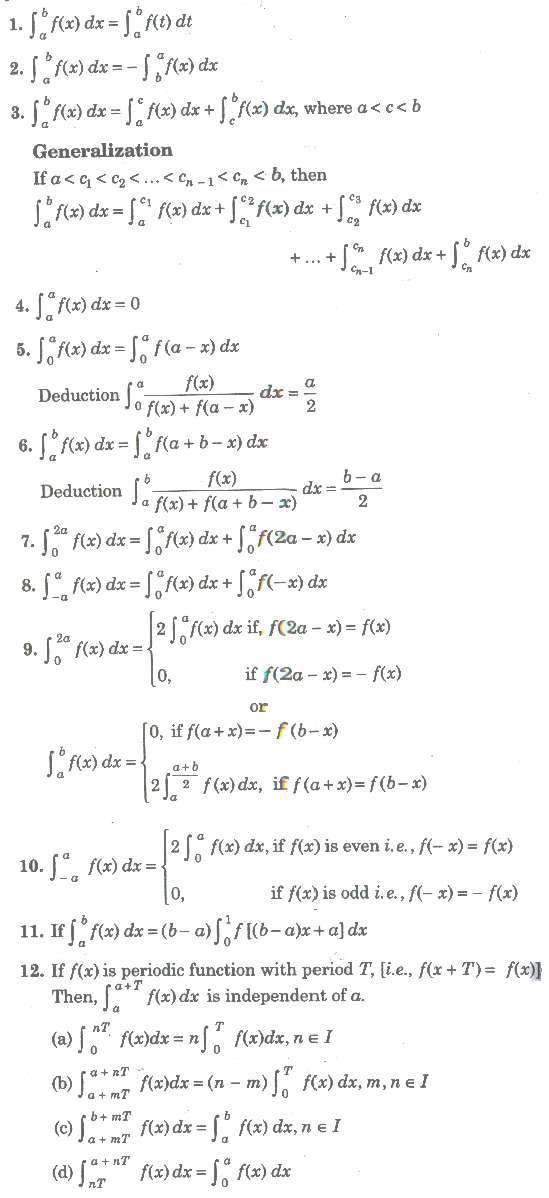
(a) If Φ(x) and ψ(x) are defined on [a, b] and differentiable for every x and f(t) is continuous, then

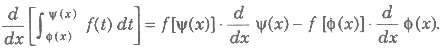
(b) If Φ(x) and ψ(x) are defined on [a, b] and differentiable for every x and f(t) is continuous, then

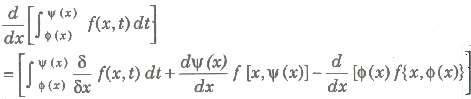
14. If f(x) ≥ 0 on the interval [a, b], then

15. If (x) ≤ Φ(x) for x ∈ [a, b], then

16. If at every point x of an interval [a, b] the inequalities g(x) ≤ f(x) ≤ h(x) are fulfilled, then

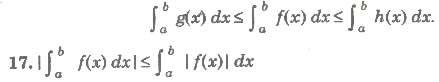
18. If m is the least value and M is the greatest value of the function f(x) on the interval [a, bl. (estimation of an integral), then

19. If f is continuous on [a, b], then there exists a number c in [a, b] at which

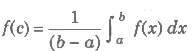
is called the mean value of the function f(x) on the interval [a, b].

20. If f²2 (x) and g² (x) are integrable on [a, b], then

21. Let a function f(x, α) be continuous for a ≤ x ≤ b and c ≤ α ≤ d.
Then, for any α ∈ [c, d], if

22. If f(t) is an odd function, thenis an even function.

23. If f(t) is an even function, thenis an odd function.

24. If f(t) is an even function, then for non-zero a,is not necessarily an odd function. It will be an odd function, if

25. If f(x) is continuous on [a, α], thenis called an improper integral and is defined as

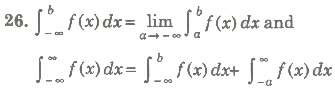
27. Geometrically, for f(x) > 0, the improper integralgives area of the figure bounded by the curve y = f(x), the axis and the straight line x = a.

Integral Function

Let f(x) be a continuous function defined on [a, b], then a function φ(x) defined byis called the integral function of the function f.

Properties of Integral Function

1. The integral function of an integrable function is continuous.
2. If φ(x) is the integral function of continuous function, then φ(x) is derivable and of φ ‘ = f(x) for all x ∈ [a, b].

Gamma Function

If n is a positive rational number, then the improper integralis defined as a gamma function and it is denoted by Γn

Properties of Gamma Function

Summation of Series by Definite Integral

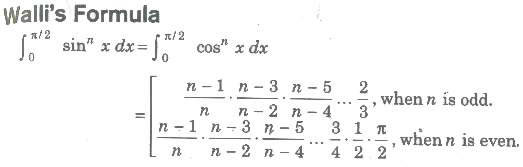
The method to evaluate the integral, as limit of the sum of an infinite series is known as integration by first principle.

Area of Bounded Region

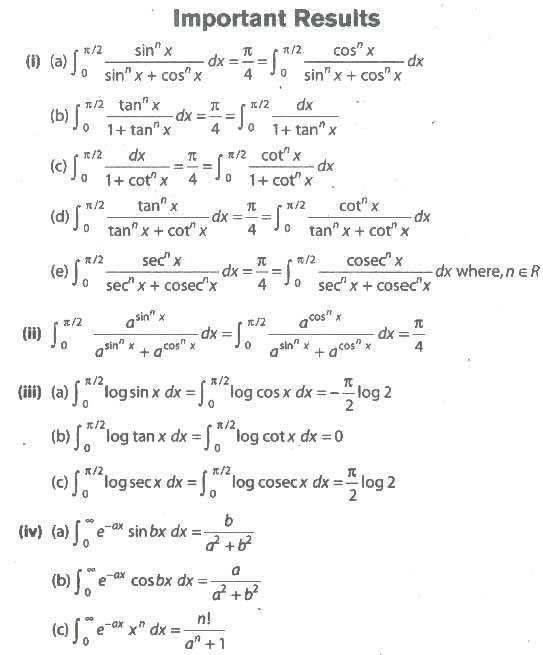
The space occupied by the curve along with the axis, under the given condition is called area of bounded region.

(i) The area bounded by the curve y = F(x) above the X-axis and between the lines x = a, x = b is given by

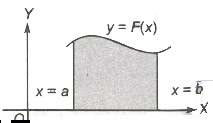
(ii) If the curve between the lines x = a, x = b lies below the X-axis, then the required area is given by

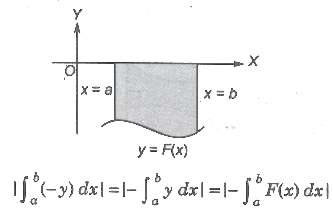
(iii) The area bounded by the curve x = F(y) right to the Y-axis and the lines y = c, y = d is given by

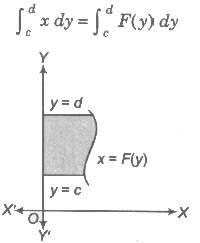
(iv) If the curve between the lines y = c, y = d left to the Y-axis, then the area is given by

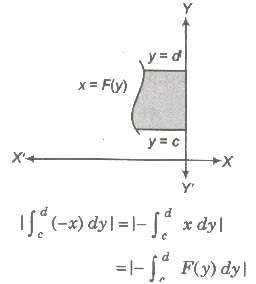
(v) Area bounded by two curves y = F (x) and y = G (x) between x = a and x = b is given by

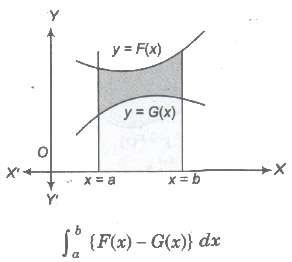
(vi) Area bounded by two curves x = f(y) and x = g(y) between y=c and y=d is given by

(vii) If F (x) ≥. G (x) in [a, c] and F (x) ≤ G (x) in [c,d], where a < c < b, then area of the region bounded by the curves is given as

Area of Curves Given by Polar Equations

Let f(θ) be a continuous function, θ ∈ (a, α), then the are t bounded by the curve r = f(θ) and <β) is

Area of Parametric Curves

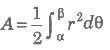
Let x = φ(t) and y = ψ(t) be two parametric curves, then area bounded by the curve, X-axis and ordinates x = φ(t₁), x = ψ(t₂) is

Volume and Surface Area

If We revolve any plane curve along any line, then solid so generated is called solid of revolution.

1. Volume of Solid Revolution

1. The volume of the solid generated by revolution of the area bounded by the curve y = f(x), the axis of x and the ordinatesit being given that f(x) is a continuous a function in the interval (a, b).
2. The volume of the solid generated by revolution of the area bounded by the curve x = g(y), the axis of y and two abscissas y = c and y = d isit being given that g(y) is a continuous function in the interval (c, d).

Surface of Solid Revolution

(i) The surface of the solid generated by revolution of the area bounded by the curve y = f(x), the axis of x and the ordinates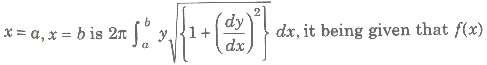is a continuous function in the interval (a, b).

(ii) The surface of the solid generated by revolution of the area bounded by the curve x = f (y), the axis of y and y = c, y = d iscontinuous function in the interval (c, d).

Curve Sketching

1. symmetry

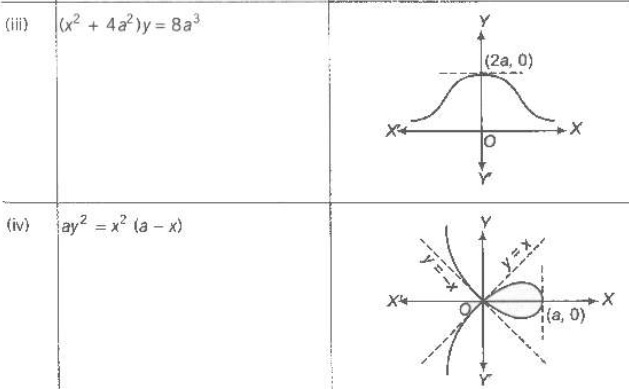
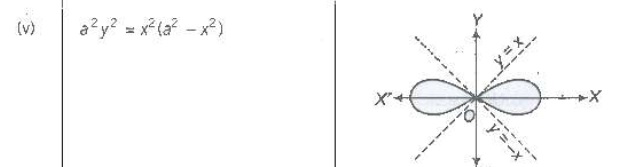
1. If powers of y in a equation of curve are all even, then curve is symmetrical about Xaxis.
2. If powers of x in a equation of curve are all even, then curve is symmetrical about Yaxis.
3. When x is replaced by -x and y is replaced by -y, then curve is symmetrical in opposite quadrant.
4. If x and y are interchanged and equation of curve remains unchanged curve is symmetrical about line y = x.

2. Nature of Origin

1. If point (0, 0) satisfies the equation, then curve passes through origin.
2. If curve passes through origin, then equate low st degree term to zero and get equation of tangent. If there are two tangents, then origin is a double point.

3. Point of Intersection with Axes

1. Put y = 0 and get intersection with X-axis, put x = 0 and get intersection with Y-axis.
2. Now, find equation of tangent at this point i. e. , shift origin to the point of intersection and equate the lowest degree term to zero.
3. Find regions where curve does not exists. i. e., curve will not exit for those values of variable when makes the other imaginary or not defined.

4. Asymptotes

1. Equate coefficient of highest power of x and get asymptote parallel to X-axis.
2. Similarly equate coefficient of highest power of y and get asymptote parallel to Y-axis.

5. The Sign of (dy/dx)

Find points at which (dy/dx) vanishes or becomes infinite. It gives us the points where tngent is parallel or perpendicular to the X-axis.

6. Points of Inflexion

and solve the resulting equation.If some point of inflexion is there, then locate it exactly.

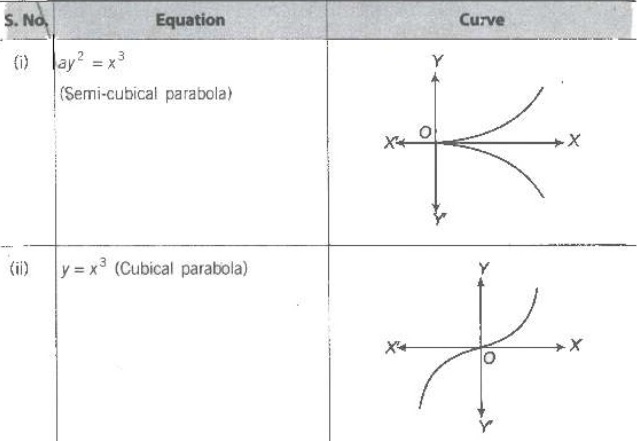
Taking in consideration of all above information, we draw an approximate shape of the curve

Shape of Some Curves is Given Below

Ncert Solution for class 6 to 12 download in pdf