NCERT Solutions Class 9 Mathematics Triangles Exercise 6.2

Concept Chapter 6 Class 9 Maths LINES AND ANGLES Ncert Solutions

Axioms of Chapter 6

Axiom 6.1 :If a ray stands on a line, then the sum of two adjacent angles so
formed is 180°
Axiom 6.2 :If the sum of two adjacent angles is 180°, then the non-common arms
of the angles form a line
Axiom 6.3 :If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Axiom 6.3 is also referred to as the corresponding angles axiom.
Axiom 6.4 : If a transversal intersects two lines such that a pair of corresponding
angles is equal, then the two lines are parallel to each other.

Theorem 6. 1 :If two lines intersect each other, then the vertically opposite angles are equal
Given :-two lines intersect each other
To prove :- ∠AOC = ∠BOD and ∠AOD = ∠BOC

Proof :- AB and CD be two lines intersecting at O as shown in Fig 6 8 They lead to two pairs of
vertically opposite angles, namely, (i) ∠AOC and ∠ BOD
(ii) ∠ AOD and ∠ BOC

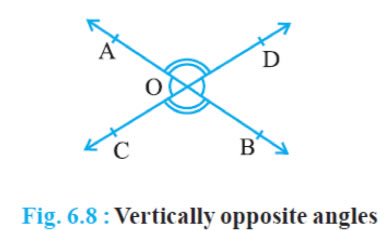
We need to prove that ∠AOC = ∠BOD
and ∠AOD = ∠BOC
Now, ray OA stands on line CD
From (Linear pair axiom)
∠AOC + ∠AOD = 180° … (1)
∠AOD + ∠BOD = 180° … (2)
From (1) and (2), we can write
∠AOC + ∠AOD = ∠AOD + ∠BOD
This implies that ∠AOC = ∠BOD
Similarly, it can be proved that ∠AOD = ∠BOC

Parallel Lines and a Transversal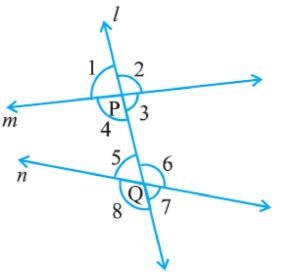

∠1, ∠ 2, ∠7 and ∠ 8 are called exterior angles,
∠ 3, ∠ 4, ∠ 5 and ∠6 are called interior angles
(a) Corresponding angles :
(i) ∠1 = ∠ 5 (ii) ∠ 2 = ∠ 6 (iii) ∠ 4 = ∠ 8 (iv) ∠ 3 = ∠ 7
(b) Alternate interior angles :
(i) ∠ 4 = ∠ 6 (ii) ∠ 3 = ∠ 5
(c) Alternate exterior angles:
(i) ∠1 = ∠ 7 (ii) ∠ 2 = ∠8
(d) Interior angles on the same side of the transversal:
(i) ∠4 + ∠5 =180°(ii) ∠3 + ∠ 6 =180°

Theorem 6.2 :If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal.
Theorem 6.4 : If a transversal intersects two parallel lines, then each pair ofinterior angles on the same side of the transversal is supplementary.

Theorem 6.5 :If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Theorem 6.6 :Lines which are parallel to the same line are parallel to each other.
Theorem 6.7 : The sum of the angles of a triangle is 180º.
Theorem 6.8 :If a side of a triangle is produced, then the exterior angle soformed is equal to the sum of the two interior opposite angles.

Exercise 6.1 Chapter 6 Class 9 Maths LINES AND ANGLES Ncert Solutions

Question 1. In Fig. 6.13, lines AB and CD intersect at O. If
∠ AOC + ∠ BOE = 70° and ∠ BOD = 40°, find
∠ BOE and reflex ∠ COE.

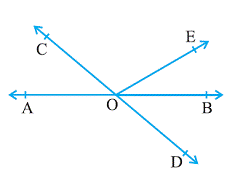
Answer:

(sum of angle in linear pair always equal to 180 )
∠AOC + ∠COE + ∠BOE = 180°
Given that ∠ AOC + ∠ BOE = 70° plug this value we get
= > 70° + ∠COE = 180°
= > ∠ COE = 180° -70°
= > ∠ COE = 110°
Also
(sum of angle in linear pair always equal to 180° )
∠COE + ∠BOE + ∠BOD = 180°

Put ∠COE = 110° and ∠ BOD = 40° we get
110° + ∠BOE + 40° = 180°
= > ∠BOE = 180° - 110° - 40°
= > ∠BOE = 30°

Question 2. In Fig. 6.14, lines XY and MN intersect at O. If
∠ POY = 90° and a : b = 2 : 3, find c.

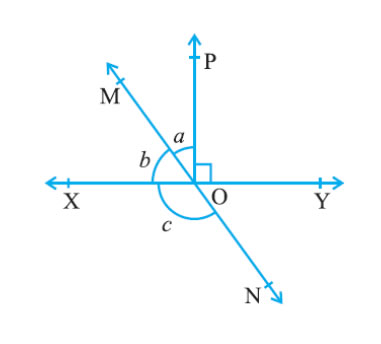
Answer:

Let ∠ a = 2x, then ∠b = 3x
(sum of angle in linear pair always equal to 180° )
∠XOM + ∠MOP + ∠POY = 180°
∠b + ∠a + ∠POY = 180°
given that ∠POY = 90°
plug this value we get
3x + 2x + 90° = 180°
5x = 90°
x = 18°
a = 2x = 2 × 18 = 36°
b = 3x = 3 ×18 = 54°
MN is a straight line.
sum of angle in linear pair always equal to 180°
so that ∠b + ∠c = 180°
54° + ∠c = 180°
∠c = 180° − 54° = 126°
∠ c = 126°

Question 3. In Fig. 6.15, ∠ PQR = ∠ PRQ, then prove that
∠ PQS = ∠ PRT.

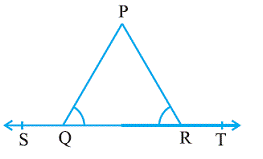
Solution:
ST is a straight line and sum of angle in linear pair always equal to 180
∠PQS + ∠PQR = 180° … (1)
And
∠PRT + ∠PRQ = 180° … (2)
From equation (1) and (2).we get:
∠PQS + ∠PQR = ∠PRT + ∠PRQ … (3)
But given that ∠PQR = ∠PRQ
Plug the value we get
∠PQS + ∠PRQ =∠PRT + ∠PRQ
∠PQS = ∠PRT + ∠PRQ - ∠PRQ
∠PQS = ∠PRT
Hence proved

Question 4. In Fig. 6.16, if x + y = w + z, then prove that AOB is a line.

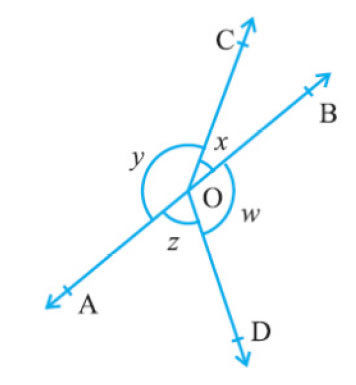
Solution: Sum of all angles in a circle always 360°
Hence
∠AOC + ∠BOC + ∠DOB + ∠AOD = 360°
=> x + y + w + z = 360°
=> x + y + x + y = 360°
Given that x + y = w + z
Plug the value we get
=> 2w + 2z = 360°
=> 2(w + z) = 360°
w + z = 180° (linear pair)
or ∠BOD + ∠AOD = 180°
If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line
Hence AOB is a line.

Question 5. In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays
OP and OR. Prove that ∠ ROS = 1/2(∠ QOS – ∠ POS).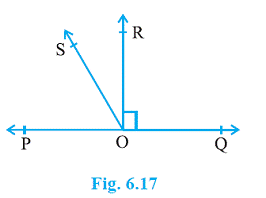

Solution
It is given that OR is perpendicular to PQ
So that ∠POR = 90°
sum of angle in linear pair always equal to 180°
∠POS + ∠SOR + ∠POR = 180°
Plug ∠POR = 90°
90°+∠SOR + ∠POR = 180°
∠SOR + ∠POR = 90°
∠ROS = 90° − ∠POS … (1)
∠QOR = 90°
Given that OS is another ray lying between rays
OP and OR so that
∠QOS − ∠ROS = 90°
∠ROS = ∠QOS − 90° … (2)
On adding equations (1) and (2), we obtain
2 ∠ROS = ∠QOS − ∠POS
∠ROS = 1/2(∠QOS − ∠POS)

Question 6. It is given that ∠ XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ ZYP, find ∠ XYQ and reflex ∠ QYP.

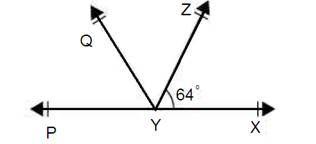
Solution: It is given that line YQ bisects ∠PYZ.
Hence,
∠QYP = ∠ZYQ
PX is straight line
sum of angle in linear pair always equal to 180°
∠XYZ + ∠ZYQ + ∠QYP = 180°
Give that so plug the value we get ∠ XYZ = 64°
And ∠QYP = ∠ZYQ
∠ 64° + 2∠QYP = 180°
∠2∠QYP = 180° − 64° = 116°
Divide by 2 we get
∠QYP = 58°
Also, ∠ZYQ = ∠QYP = 58°
Using angle of reflection
∠QYP = 360° − 58° = 302°
∠XYQ = ∠XYZ + ∠ZYQ
= 64° + 58°
= 122°

Exercise 6.2 Chapter 6 Class 9 Maths LINES AND ANGLES Ncert Solutions

Question 1. In Fig. 6.28, find the values of x and y and then show that AB || CD.

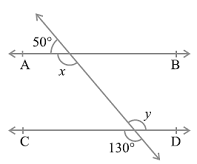
Solution:

50° + x = 180° (sum of angle in linear pair is 180° )
x = 180° -50°
x= 130°

y is vertical opposite angle of 130° so that
y = 130°

Question 2. In Fig. 6.29, if AB || CD, CD || EF and y : z = 3 : 7, find x.

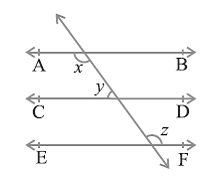
Solution:

Given that y : z = 3 : 7
Let ∠ y = 3a
Then ∠z = 7a
∠x and ∠z are alternate interior angles of parallel lines so that
∠x = ∠z …(1)
Sum of interior angle on the same side of the transversal is always = 180°
So that
x + y = 180°
plug the value of x from equation (1)
z + y = 180°
plug the value of z and y we get
7a + 3a = 180°
10 a = 180°
a = 180°/10
a = 18

y = 3a = 3x18 = 54°
z = 7a = 7x18 = 126°
x = z = 126°

Question 3. In Fig. 6.30, if AB || CD, EF ⊥ CD and ∠ GED = 126°, find ∠ AGE, ∠ GEF and ∠ FGE.

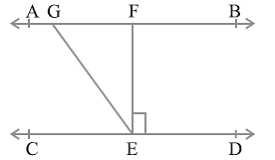
Solution :
∠GEF + ∠FEG = ∠GED
EF ⊥ CD so that ∠ FED = 90°
And given that ∠ GED = 126°
Plug the values we get
∠GEF + 90° = 126°
∠GEF = 126°- 90°
∠GEF = 36°

AB || CD, EF ⊥ CD so ∠EFG = 90°
Use angle sum property of triangle (sum is 180°)
∠GEF + ∠EFG + ∠FGE = 180°
Plug the values we get
36° + 90° + ∠FGE = 180°
∠FGE = 180° – 36° - 90°
∠FGE = 54°

AB is a straight line so that use linear pair property
∠AGE +∠FGE = 180°
Plug the value of ∠FGE = 54°
We get
∠AGE +54° = 180°
∠AGE = 180° - 54°
∠AGE = 126°

Question 4. In Fig. 6.31, if PQ || ST, ∠ PQR = 110° and ∠ RST = 130°, find ∠ QRS.
[Hint : Draw a line parallel to ST throughpoint R.]

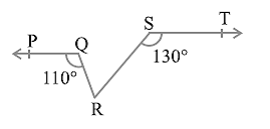
Solution: Let us draw a parallel line XY to PQ || ST and passing through point R.
Sum of interior angle on the same side of the transversal is always = 180°

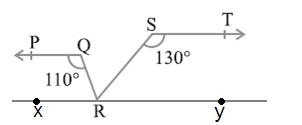
So that
∠ PQR + ∠ QRX = 180°
Given that ∠ PQR= 110°
110° + ∠QRX = 180°
∠QRX = 180° -110°
∠QRX = 70°
Sum of interior angle on the same side of the transversal is always = 180°

∠RST + ∠SRY = 180° (Co-interior angles on the same side of transversal SR)
Also
130° + ∠SRY = 180°
∠SRY = 50°
XY is a straight line. Use property of linear pair we get
∠QRX + ∠QRS + ∠SRY = 180°
70° + ∠QRS + 50° = 180°
∠QRS = 180° − 120°
= 60°

Question 5. In Fig. 6.32, if AB || CD, ∠ APQ = 50° and ∠ PRD = 127°, find x and y.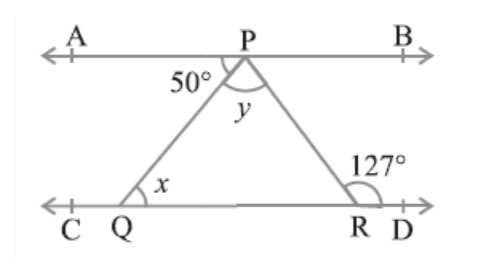

Solution: Use property of Alternate interior angles
∠APR = ∠PRD
50° + y = 127°
y = 127° − 50°
y = 77°
use same property of Alternate interior angles
∠APQ = ∠PQR
50° = x
∠ x = 50° and y = 77°

Question 6. In Fig. 6.33, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove thatAB || CD.

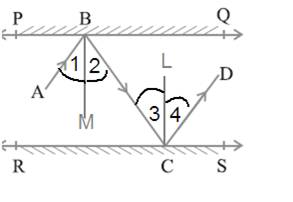
Solution: Let draw BM ⊥ PQ and CN ⊥ RS.
Given that PQ || RS so that BM || CN
Use the property of Alternate interior angles
∠2 = ∠3 … (1)
∠ABC = ∠1 + ∠2
But ∠1 = ∠2 so that
∠ABC = ∠2 + ∠2
∠ABC = 2∠2
Similarly
∠BCD = ∠3 + ∠4
But ∠3 = ∠4 so that
∠ BCD = ∠3 + ∠3
∠ BCD = 2∠3
From equation first
∠ABC = ∠DCB
These are alternate angles so that AB || CD
Hence proved

Ncert Solution for class 6 to 12 download in pdf

Follow Us On

Facebook

Twitter

Youtube

Linkdin