NCERT Solutions Class 9 Mathematics Chapter 1: Number System Exercise 1.6

Concept Chapter 1 Class 9 Maths Number System Ncert Solutions

Number System

Natural number (N) 1,2,3,4,5,………………….
Whole number (W) 0,1,2,3,4……………………
Integers (Z) ………….-3,-2,-1,0,1,2,3………
Rational number 2/3 ,5/10 , 0.001 , 0.6666 or .444444444…………….
Real numberall rational number, v2, 1/v5

Rational number :-
Numbers that can be expressed in the form p/q, where q is a non-zero integer and p is any integer are called rational numbers.
Examples 0 ,1/2 and 4/5 etc
Every integer is a-rational number but a rational number need not be an integer.
Every fraction is a rational number but a fraction need not be a rational number.

Irrational number :-
Numbers that cannot be put in the form of p/q , where q is not equal to 0
When p and q both are integers
Example √2 , √5 and √8 etc
Every fraction is a rational number but a fraction need not be a rational number.
Standard form of rational number :-
A rational number is said to be in the standard form if q is positive integer and the integers p and q have no common isor other than 1.
Example 2/5 , 7/9 etc
We can find as many rational numbers between x and y using the formula (x+y)/2
If x and y are any two rational numbers, then :
Sum or difference of two x and y will always rational
And product or ision of x and y will always rational
If one variable is rational and other is irrational in x and y then
Sum or difference of two x and y will always irrational
And product or ision of x and y will always irrational

Terminating fractions:-
Fractions which leaves remainder zero on ision. If Prime factors of the denominator are 2 or 5 or both only. Then the number will terminating

Example 7/10 is terminating as denominator 10 has prime factors 2 and 5 only
Example 3/25 is terminating as denominator 25 has prime factors 5 only

Recurring fractions:-
Fractions which never leave a remainder 0 on ision. If Prime factors of the denominator are not 2 , 5 or both only. Then the number will repeating or recurring.
Examples :-
1/15 it will recurring fraction because prime factors of denominator has 3 also other than 2 and 5

There are infinitely many rational numbers between any two rational numbers. We can calculate the rational number between two rational number x and y by (x+y)/2

Properties of rationalization

Properties to solve exponential values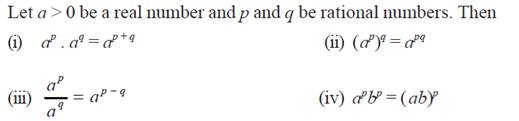

Exercise 1.1 Chapter 1 Class 9 Maths Number System Ncert Solutions

Question -1 Is zero a rational number? Can you write it in the form p/q , where p and q are integers and q ≠0?

Answer
Yes o is a rational number because it can be written in form of 0/1 , 0/2 and so on
And according to definition of rational number which can be expressed in term form of p/q when q is non zero integer and p is a integer .
And here o is an integer and 1,2 .. are non zero integers
Hence, 0 is a rational number

Question -2 Find six rational numbers between 3 and 4.
Solution: Since we want six numbers, we write 1 and 2 as rational numbers with denominator 6 + 1 =7
So multiply in numerator and denominator by 7 we get

Question -3 Find five rational numbers between 3/5 and 4/5.
Solution: Since we want five numbers, we write 3/5 and 4/5 So multiply in numerator and denominator by 5+1 =6 we get

Question 4 State whether the following statements are true or false. Give reasons for your answers.
Solution: (i)Every natural number is a whole number.
Natural number are all counting number like 1,2,3,4, …….
And whole number has 0 also in natural number so they will 0,1,2,3,4,……..
So here every natural number is a whole number

(ii)Every integer is a whole number.

Whole numbers are 0,1,2,3,……….
And integer numbers are ……… - 3, - 2 ,- 1 , 0 , 1 , 2 , 3 ………..
Hence all integers are not whole number
-3,-2,1 are integers but not whole numbers

(iii)Every rational number is a whole number.

rational number which can be expressed in term form of p/q when q is non zero integer and p is a integer .
so rational numbers are 2/5 . 0.01 , 10 ………
and here there are not whole number
so all rational number is not whole number

Exercise 1.2 Chapter 1 Class 9 Maths Number System Ncert Solutions

Question 1. State whether the following statements are true or false. Justify your answers.
Solution: (i)Every irrational number is a real number.
True a real number can either rational or irrational

(ii)Every point on the number line is of the form √m, where m is a natural number.
False all numbers can lies on number line

(iii)Every real number is an irrational number
False, all real numbers are rational number

Question 2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.
Solution: All perfect square number has rational roots
Examples √1 , √4 ,√9 ,√25 ………….

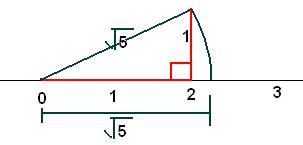
Question 3 Show how √5 can be represented on the number line.
√5 = √(4+1)
Solution: Here 4 and 1 both are perfect square number as √4 = 2 and √1 = 1
So draw right triangle with side 2 and 1
And according to Pythagoras theorem hypotenuse will √(22+12) = √5
Then draw an arc of √5 on number line

Exercise 1.3 Chapter 1 Class 9 Maths Number System Ncert Solutions

Question 1. Write the following in decimal form and say what kind of decimal expansion each has

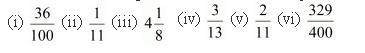
Solution: (i)36/100 = 0.36 and it is terminating.

(ii) by long ision method we get

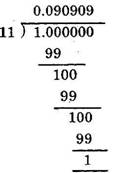
And
(iii) 1/11 = 0.090909090……….
So it is a non terminating number

4.125 is a terminating number
(iv)

We are getting 3/13 = 0.230769230769230769…..
There is repetition of 230769 so it is a non terminating number
(v)

2/11 = 0.18181818 ……..
There is repartition of 18 so it is not terminating number
(vi)

329/400 = 0.8225
So it is terminating number

Question 2 You know that 1/7 = 0.142857 bar . Can you predict what the decimal expansion of2/7 , 3/7 ,4/7 , 5/7 and 6/ 7are, without actually doing the long ision? If so, how?
[Hint:Study the remainders while finding the value of1/7carefully.]
Solution: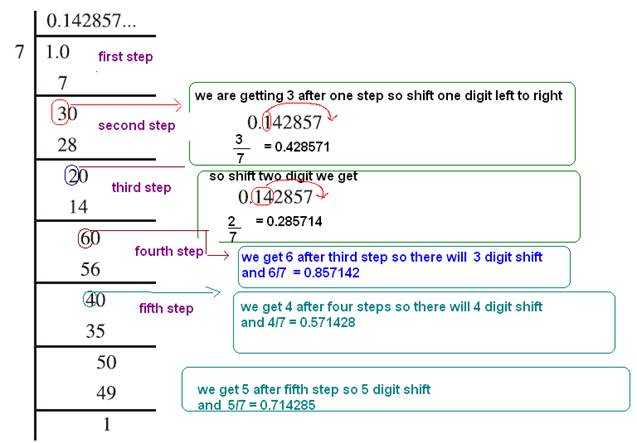

Question 3 Express the following in the form p/q , where p and q are integers and q ≠0.

Solution: (i)
Letx= 0.666…
Multiply by 10 we get
10x= 6.666…
x= 0.666…
subtract them we get

9x = 6 +x
9x= 6
Divide by 9
x=6/9
simplify it by ide 3 we get
x = 2/3 Answer

(ii)
Letx= 0.4777…
Multiply by 10 we get
10x= 4.7777…
x = 0.4777…
subtract x we get
9x = 4.3
Divide by 9

X = 4.3/9
To remove decimal add zero in denominator we get
x = 43/90

(iii)
Letx= 0.001001…
There are 3 repeating digits so multiply by 10*10*10 = 1000
1000x= 1.001001…
X = 0.001001…
subtract x there we get
999 x = 1
Divide by 999 we get
X = 1/999

Question 4 . Express 0.99999 .... in the form p/q .Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.
Solution: Letx= 0.9999…
There is only one repeating digit so multiply by 10 we get
10x= 9.9999…
x= 0.9999…
subtract x now we get
9x= 9
Divide by 9 we get
x= 9/9 = 1

Question 5 What can the maximum number of digits be in the repeating block of digits in the decimal expansion of1/17? Perform the ision to check your answer. Perform the ision to check your answer.

Question 6 Look at several examples of rational numbers in the formp / q (q≠ 0), wherepandqare integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what propertyq must satisfy? Solution: If the denominator is product of 2 and 5 only then it will always give terminating number For example7/2 = 0.35, 19/10 = 1.9, 12/5 = 2.5, 1/25 = 0.04, 1/ 4 = 0.25and you can write such many examples.

Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution: All irrational number has non terminating and non and recurring decimal expressions
So √2 , √3 ,√5 all will give such decimal expansions

Question 8: Find three different irrational numbers between the rational numbers5/7and9/11
Solution: Divide the number we get
5/7 = 0.71….
9/11= 0.81…..

So we can write many irrational numbers between both values like
0.720720072000……
0.730730073000……
0.740740074000…….
0.757507500750000………..

Question 9. Classify the following numbers as rational or irrational:

Solution:
(i) 23 is not a perfect square values so that, it is an irrational number.

(ii)√(225) = √(3*3*5*5)
Pairs comes outside the root and we get
√(3*3*5*5) = 15
That means 225 is a perfect square value so it a rational number
(iii) 0.3796
The decimal expansion of above number is terminating, so that it is a rational number.
(iv) 7.478478 …
The decimal expansion of above number is non-terminating recurring, so that, it is a rational number.
(v) 1.10100100010000 …
The decimal expansion of above number is non-terminating non-repeating, so that , it is an irrational number.

Exercise 1.4 Chapter 1 Class 9 Maths Number System Ncert Solutions

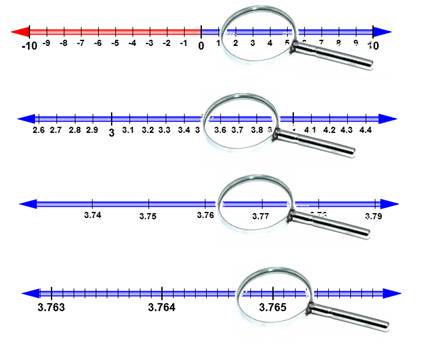
Question 1. Visualise 3.765 on the number line, using successive magnification.

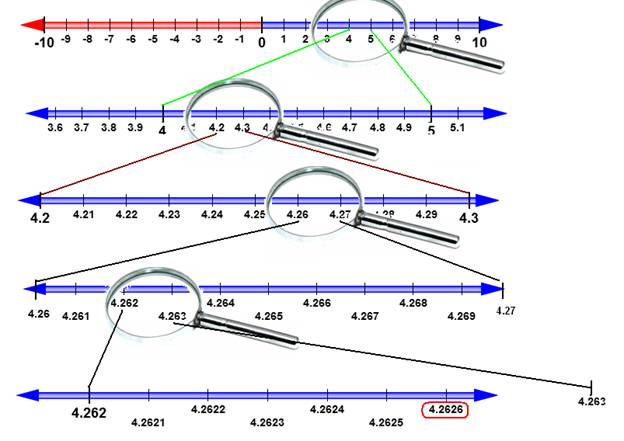
Question 2. Visualize 4.26 on the number line, up to 4 decimal places.

Exercise 1.5 Chapter 1 Class 9 Maths Number System Ncert Solutions

Question 1. Classify the following numbers as rational or irrational:

Solution: (i)2 - √5

Here 2 is a rational number and √5 is a irrational number
And difference of rational and irrational is always a irrational number
So that 2 - √5 is a irrational number

(ii) (3 + √23) - √23

Solve the bracket we get

3 + √23 - √23 = 3

and 3 is a rational number so that (3 + √23) - √23 is a rational number

(iii) and 2/7 can be written in form of p/q so it a rational number

(iv) 1/ √2 is an irrational number because 1 is rational and √2 is irrational and product or ision of rational with irrational is always irrational

(v) 2pi it is an irrational here 2 is rational and pi is a irrational number and product or ision of rational with irrational is always irrational

Question 2: Simplify each of the following expressions:

Solution:

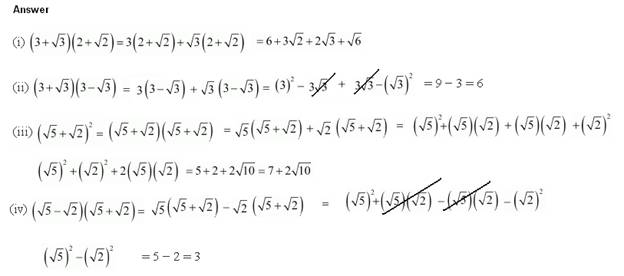
Question 3: Recall, π is defined as the ratio of the circumference (sayc) of a circle to its diameter (sayd). That is,. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Solution: There is no contradiction.. We can never obtain an exact value of c and d so that , either cordis irrational. and product or ision of rational with irrational is always irrational . Therefore, the fractionc/dis irrational. Hence, π is irrational.

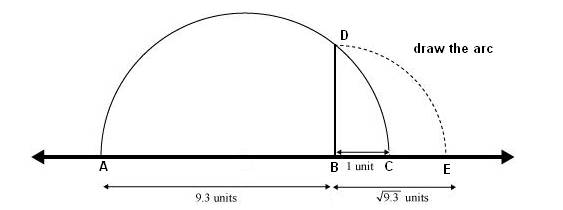
Question 4. Represent√9.3on the number line

Solution:
Draw a line segment AB of length 9.3 units
Extend the line 1 unit more such that BC = 1 units
Find the midpoint of AC
Draw semicircle with center O and radius OC
Draw a line BD perpendicular to AB, intersecting the semicircle at point D
Here BD = √9.3 to represent it in number line draw a arc DE such that BE= BD
Here BE is our required line

Question 5 Rationalize the denominator of the followings

Solution:

Exercise 1.6 Chapter 1 Class 9 Maths Number System Ncert Solutions

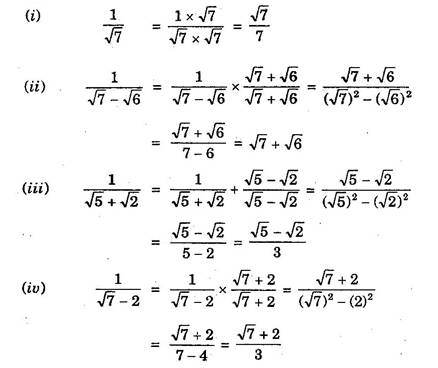
Question 1. Find (i) 64^1/2 (ii) 32^1/5 (iii)125^1/3
Solution:

Question 2. find (i) 9^3/2 (ii)32^2/5 (iii)16^3/4 (iv)125^-1/5
Solution:

Question 3 Simplify : (i) 2^2/3.2^1/5 (ii)(1/3³)⁷ (iii)11^1/2/11^1/4 (iv)7^1/2.8^1/2
Solution:

Ncert Solution for class 6 to 12 download in pdf