NCERT Solutions Class 12 Physics 1. ELECTRIC CHARGES AND FIELDS Exercise

Formula Chapter 1 Class 12 Chemistry PhysicsELECTRIC CHARGES AND FIELDS Ncert Solutions

Physics Formula - 1
Apply Coulomb’s law

q₁ = first charge
q₂ = Second charge
r = distance between both charge
ε0= permittivity of free space
1/4πε0 = 9 x 10⁹ Nm²C^-2

Physics Formula - 2
Coulomb’s force law between two point charges q₁ and q₂ located at r₁ and r₂ is then expressed as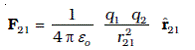

Physics Formula - 3

Thus the total force F1 on q₁ due to the two charges q₂ and q3 is given as

Physics Formula - 4

Resultant force

Physics Formula - 5

The electric field produced by the charge Q at a point r is given as

Physics Formula - 6

Force F exerted by a charge Q on a charge q

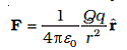
Physics Formula - 7

The electric field E at r due to the system of charges is

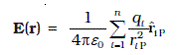
Physics Formula - 8

The total flux φ through a surface S is
φ ≈ Σ E.ΔS
Physics Formula - 9
the electric field of a dipole at large distances takes simple forms:
At a point on the dipole axis

At a point on the equatorial plane

Physics Formula - 10
Surface charge density σ at the area element by

Physics Formula - 1 1
The linear charge density of a wire is defined by

Physics Formula - 1 2
The volume charge density (sometimes simply called charge density) is defined as

Physics Formula - 1 3
Electric field due to the charge ρΔV is given by Coulomb’s law:

Physics Formula - 1 4
The total electric field due to the charge distribution is obtained by summing over electric fields due to different volume elements:

Physics Formula - 1 5
Total flux through a sphere of radius r, which encloses a point charge q at its centre.

Physics Formula - 1 6
Electric flux through a closed surface S
∆ φ1 = q/ε0
Physics Formula - 1 7
Flux through the Gaussian surface

Physics Formula - 1 8
Field due to a uniformly charged infinite plane sheet

n is a unit vector normal to the plane and going away from it
Physics Formula - 1 9
Field outside the shell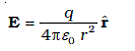


E=0

Exercise Chapter 1 Class 12 Chemistry PhysicsELECTRIC CHARGES AND FIELDS Ncert Solutions

Question 1: What is the force between two small charged spheres having charges of 2 × 10⁻⁷ C and 3 × 10⁻⁷ C placed 30 cm apart in air?
Solution:

Given that
Charge on the first sphere, q₁ = 2 × 10⁻⁷ C
Charge on the second sphere, q₂ = 3 × 10⁻⁷ C
Distance between the spheres, r = 30 cm =30/100 m = 0.3 m
(ide by 100 to convert cm to m )
Apply Coulomb’s law

q₁ = first charge
q₂ = Second charge
r = distance between both charge
ε₀= permittivity of free space
1/4πε₀ = 9 × 10⁹ Nm²C^-2
Plug the values in formula we get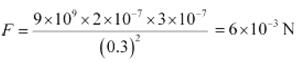

Answer
Attraction force between both charges is 6 × 10⁻³ N.

Question 2:The electrostatic force on a small sphere of charge 0.4 µC due to another small sphere of charge − 0.8 µC in air is 0.2 N. (a) What is the distance between the two spheres? (b) What is the force on the second sphere due to the first?
Solution:
(a) What is the distance between the two spheres?
Given that
Charge on first small sphere, q₁ = 0.4 µC = 0.4 × 10⁻⁶ C
Charge on second small sphere, q₂ = − 0.8 µC = − 0.8 × 10⁻⁶ C
(1µC = 10 ^–6C so multiply by 10^-6 there)
The electrostatic force on a small sphere, F = 0.2 N

Apply Coulomb’s law

q₁ = first charge
q₂ = Second charge
r = distance between both charge
ε₀= permittivity of free space
1/4πε₀ = 9 × 109 Nm2C-2
Plug the values we get

The distance between the two spheres is 0.12 m.

(b) What is the force on the second sphere due to the first?
Both charge will attract each other with the same force. Hence, attraction force on the second charged sphere due to the first charged sphere is 0.2 N.

Question 3:Check that the ratio ke²/G m_em_p is dimensionless. Look up a Table of physical constants and determine the value of this ratio. What does the ratio signify?
Solution:
Use the table of physical constants we get
Unit of
G = N m² kg⁻².
me = Kg
mp = Kg (Masses of electron and proton)
e = C (e is electric charge)
k = 1/4πε₀ = Nm²C^-2
Plug the values of the units, we get

= N⁰m⁰C⁰Kg⁰

All units have canceled out hence it is a ratio, because ratio has no unit

Values of all variable or constant
Charge in electron , e = 6 × 10⁻¹⁹ C
Gravitational constant G = 6.67 × 10−11 N m² kg^-2
Mass of electron, m_e= 9.1 × 10⁻³¹ kg
Mass of proton , m_p = 1.66 × 10⁻²⁷ kg
Plug the values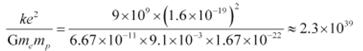

Ratio is nearly equal to 2.3 × 10 ³⁹.

Question 4: (a) Explain the meaning of the statement ‘electric charge of a body is quantised’.
(b) Why can one ignore quantisation of electric charge when dealing with macroscopic i.e., large scale charges?

Solution:

(a) The meaning of the statement ‘electric charge of a body is quantised’ is that only integral number of electrons can be transferred from one body to the other which is 1,2,3, …….. . In other word we can say that fractional number of electron can not transfer from one body to another body. Hence, the electrical charge contain by any body will be multiple of integrals.

(b) In macroscopic or large scale charges, the charges used are huge as compared to the magnitude of electric charge. Hence, quantization of electric charge is of no use on macroscopic scale. Therefore, it is ignored and it is considered that electric charge is continuous.

Question 5:When a glass rod is rubbed with a silk cloth, charges appear on both. A similar phenomenon is observed with many other pairs of bodies. Explain how this observation is consistent with the law of conservation of charge.
Solution:
When a glass rod is rubbed with a silk cloth, both bodies get equal charge with opposite nature. Equal amount of charge with opposite nature will cancel out each other. Hence sum of charge is equal to 0.
Hence this activity follow the law of conservation of charge.
Same phenomenon will observed with many other pairs of bodies

Question 6:Four point charges qA = 2 µC, qB = −5 µC, qC = 2 µC, and qD = −5 µC are located at the corners of a square ABCD of side 10 cm. What is the force on a charge of 1 µC placed at the centre of the square
Solution:
Given that
A square ABCD with each side = 10 cm = 0.1 m (ide by 100 to convert cm to m )
Charge qA = 2 µC, qB = −5 µC, qC = 2 µC, and qD = −5
And 1 µC placed at the centre of the square

Draw the figure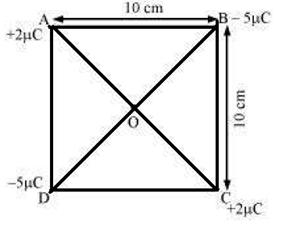

Apply Coulomb’s law

q₁ = first charge
q₂ = Second charge
r = distance between both charge
ε₀= permittivity of free space
From the figure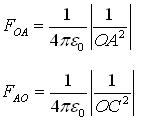

We know that OA = OC hence
FOA = - FOC
FOA + FOC = 0
Similarly
FOB + FODC = 0
Similarly other forces will also cancel out to each other
F_TOTAL =0
Hence sum of all forces w =0

Question 7:(a) An electrostatic field line is a continuous curve. That is, a field line cannot have sudden breaks. Why not?
(b) Explain why two field lines never cross each other at any point?
Solution:

(a) An electrostatic field line is a continuous curve because

When a charge goes in electrostatic field, charge experiences a continuous force. The charge moves continuously so that the field line cannot contain sudden breaks and charge can not jump from one point to the other suddenly.

(b) The electric field intensity can not show two directions at a position. Hence two lines can never cross to each other.

Question 8: Two point charges qA = 3 µC and qB = −3 µC are located 20 cm apart in vacuum.
(i) What is the electric field at the midpoint O of the line AB joining the two charges?
(ii) If a negative test charge of magnitude 1.5 × 10⁻⁹ C is placed at this point, what is the force experienced by the test charge?
Solution: Given that

qA = 3 µC = 3 × 10 ^–6 C
qB = −3 µC = - 3 × 10 ^–6 C
Distance AB = 20 cm = 0.2 m
In this problem, O is the mid-point of line AB.
OB = OA = 0.2/2 = 0.1 m
The electric field produced by the charge Q at a point r is given as

Plug the values we get
Electric field at point O caused by +3µC charge,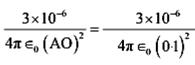

Magnitude of electric field at point O caused by −3µC charge,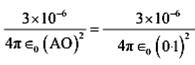

The direction of electric field is always positive to negative so that
Direction of electric field will in direction of OB

Total electric field due to both charge
E _total = E₁ + E₂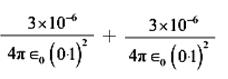

Plug 1/4πε₀ = 9 × 10⁹ Nm²C^-2
We get
E total = 5.4 × 10⁶ N/C along OB
Answer
The electric field at mid-point O is 5.4 × 10⁶ N C⁻¹ along the direction OB.

(ii) A test charge of amount 1.5 × 10⁻⁹ C is placed at mid-point O. q = 1.5 × 10⁻⁹ C

Given that
q = 1.5 × 10⁻⁹ C
Force experienced by the test charge = F
Use formula of electrostatic force of attraction
F = qE
Plug the values in this formula we get
F = 1.5 × 10⁻⁹ × 5.4 × 10⁶ = 8.1 × 10⁻³ N
Here placed charge is negative so negative charge at point B will repel while positive change at point A will attract. Hence the direction of force will along OA
Answer
The force experienced by the test charge = 8.1 × 10⁻³ N along the direction of OA.

Question 9: A system has two charges q_A = 2.5 × 10⁻⁷ C and q_B = −2.5 × 10⁻⁷ C located at points A: (0, 0, − 15 cm) and B: (0, 0, + 15 cm), respectively. What are the total charge and electric dipole moment of the system?
Solution:
Given that
q_A = 2.5 × 10⁻⁷ C
q_B = −2.5 × 10⁻⁷ C
A: (0, 0, − 15 cm)
B: (0, 0, + 15 cm),
The value of x and y coordinate is zero in both points A and B
So both points are in straight line
And the distance between both points is = 15 – (-15) = 30 cm = 0.30 m
Total charge of the system will
q = q_A + q_B
= 2.5 × 10⁷ C − 2.5 × 10⁻⁷ C
= 0

The formula of electric dipole moment of the system
p = charge × d
= q_A × d
= 2.5 × 10⁻⁷ × 0.3
= 7.5 × 10⁻⁸ C m

In this problem negative charge is along positive z-axis
Answer
7.5 × 10⁻⁸ C m along positive z−axis.

Ncert Solution for class 6 to 12 download in pdf