
Ncert Solutions for class 12 subject Maths Chapter 8 APPLICATION OF INTEGRALSin pdf Best Free NCERT Solutions for class 1 to 12 in pdf NCERT Solutions, cbse board, Maths, ncert Solutions for Class 12 Maths, class 12 Maths ncert solutions, APPLICATION OF INTEGRALS, Class 12, ncert solutions chapter 8 APPLICATION OF INTEGRALS, class 12 Maths, class 12 Maths ncert solutions, Maths ncert solutions class 12, Ncert Solutions Class 12 Mathematics Chapter 8 APPLICATION OF INTEGRALS
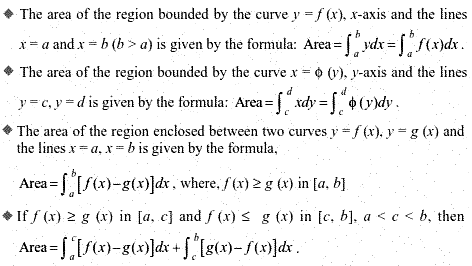
1. Find the area of the region bounded by the curve y^2 =x and the lines x = 1 , x = 4 and the x axis
2.Find the area of the region bounded by y^2 = 9x, x=2, x =4 and the x axis in the first quadrant.
Find the area of the region bounded byFind the equation of the region bounded by the ellipse x^2/16 + y^2/9 =1
Find the equation of the region bounded by the ellipse x^2/4 + y^2/9 =1
6. find the area of the region in the first quadrant enclosed by x axis, line x =root 3 y and the circle x^2 + y^2 = 4
7.Area between x=y2 and x=4 is divided in two equal parts by the line x = a, find the value of a
8. The area between x^2 = y and x = 4 is divided into two equal parts by the line x = a, find the value of a.
9. Find the area of the region bounded by the parabola y = x^2 and y= |x|
10. Find the area bounded by the curve x^2 =4y and the line x = 4y- 2
11. Find the area of the region bounded by the curve y2 = 4x and the line x = 3.
12. Area lying in the first quadrant and bounded by the circle x2 + y = 4 and the lines x = 0 and x = 2 is 2
13. Area of the region bounded by the curve y^2 =4x , y axis and the line y=3 is
1. Find the area of the circle 4x^2 + 4y^2 = 9 which is interior to the parabola x^2 =4y
2. Find the area bounded by curves (x – 1)^2 + y^2 = 1 and x^2 + y^2 = 1
3.Find the area of the region bounded by the curves y= x^2 + 2 , y=x , x =0 and x = 3
4.Using integration find the area of region bounded by the triangle whose vertices are (– 1, 0), (1, 3) and (3, 2).
5. Using integration find the area of the triangular region whose sides have the equations y = 2x + 1, y = 3x + 1 and x = 4.
6. Smaller area enclosed by the circle x^2 +y^2 = 4 and the lines x + y = 2 is (A) 2 (π – 2) (B) π – 2 (C) 2π – 1 (D) 2 (π + 2)
7. Area lying between the curves y^2 = 4x and y = 2x is
1. Find the area under the given curves and given lines (i) y = x^2 , x=1 , x= 2 and x axis (ii) y = x^4 , x=1 , x= 5 and x axis
2. Find the area between the curves y = x and y = x^2
3.Find the area of the region lying in the first quadrant and bounded by y = 4x^2, x=0, y=1 and y= 4
4. Sketch the graph of y = x + 3 and evaluate integration limits 6 to 0 of x + 3 dx
5. Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
6. Find the area enclosed between the parabola y^2 = 4ax and the line y =mx
7. Find the area enclosed by the parabola 4y = 3x^2 and the line 2y = 3x + 12 using integration to find area,
8. Find the area of the smaller region bounded by the ellipse x^2/9 + y^2/4 = 1 and the line x/3 + y/2 =1
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.