
Ncert Solutions for class 12 subject Maths Chapter 4 DETERMINANTSin pdf Best Free NCERT Solutions for class 1 to 12 in pdf NCERT Solutions, cbse board, Maths, ncert Solutions for Class 12 Maths, class 12 Maths ncert solutions, DETERMINANTS, Class 12, ncert solutions chapter 4 DETERMINANTS, class 12 Maths, class 12 Maths ncert solutions, Maths ncert solutions class 12, Ncert Solutions Class 12 Mathematics Chapter 4 DETERMINANTS
Question 1. Evaluate the determinants in Exercises 1 and 2.
Answer:
Use formula

= 2(−1) − 4(−5) = − 2 + 20 = 18
Question 2. Evaluate the determinants in Exercises 1 and 2.

Answer
Use formula
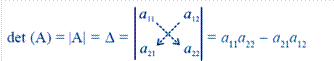
= (cos θ)(cos θ) − (−sin θ)(sin θ) = cos2 θ+ sin2 θ = 1
(ii)
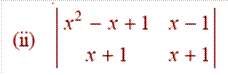
Use formula

= (x2 − x + 1)(x + 1) − (x − 1)(x + 1)
= x3 − x2 + x + x2 − x + 1 − (x2 − 1)
= x3 + 1 − x2 + 1
= x3 − x2 + 2
Question 3. If  , then show that | 2A | = 4 | A |
, then show that | 2A | = 4 | A |
Answer:
LHS
|2A| = 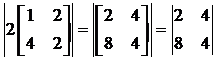
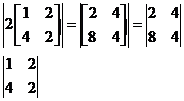
Use formula 
=2(4) – 4(8)
= 8 – 32
= - 24
R.H.S
4|A| = 4![]() = 4(1 x 2 - 2 x 4 )
= 4(1 x 2 - 2 x 4 )
= 4(2 – 8)
= 4(-6)
= - 24
L.H.S = R.H.S
Hence proved
Question 4. If , then show that | 3 A | = 27 | A |
, then show that | 3 A | = 27 | A |
Answer:
LHS
=>|3A| = 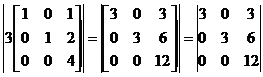
Use formula
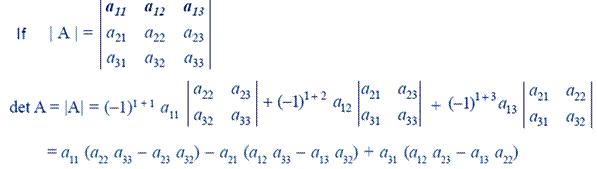
=>|3A| = 3(36 - 0) – 0(0 -0) + 3(0-0)
= 108
R.H.S
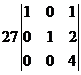 = 27{1(4 - 0) – 0(0 -0) + 1(0-0)}
= 27{1(4 - 0) – 0(0 -0) + 1(0-0)}
= 27 x 4
= 108
LHS = RHS
Hence proved
Question 5. Evaluate the determinants


Solution: (i)
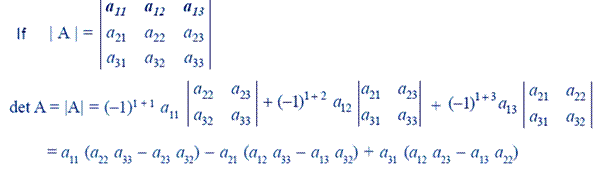
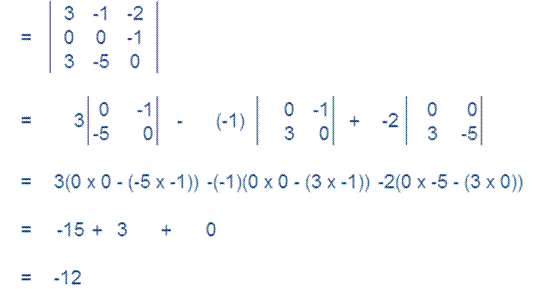
(ii)
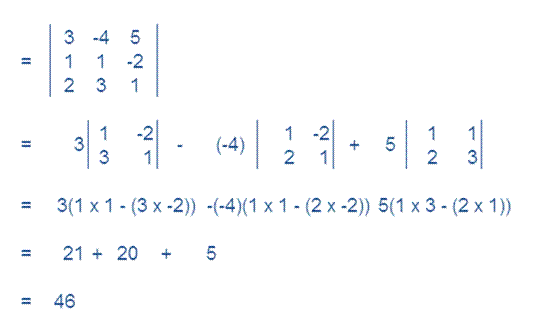
(III)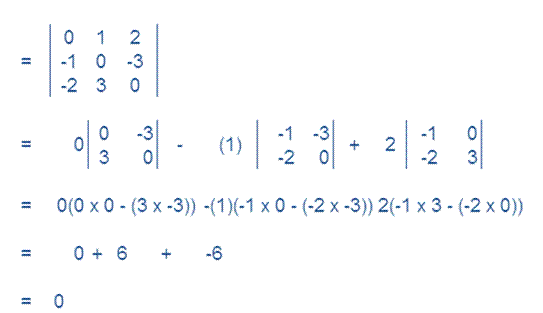
(IV)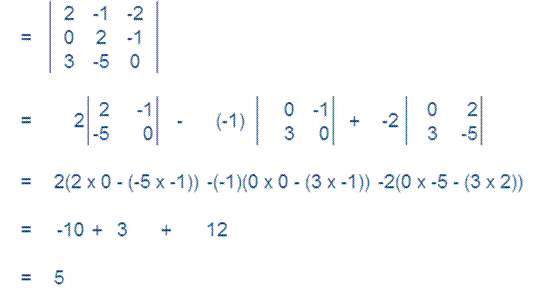
Question 6. If  , find | A |
, find | A |
Answer: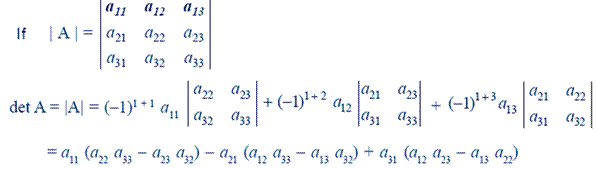
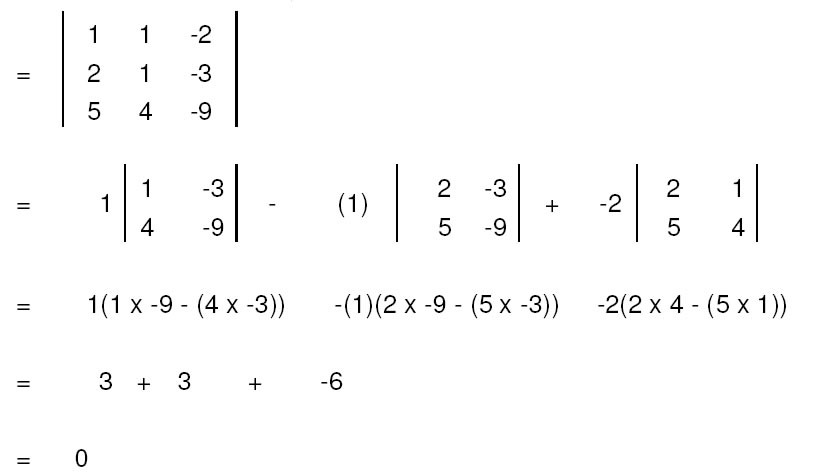
Question 7. Find values of x, if
Solution: (i)
2(1) - 5(4) = 2x(x) – 6(4)
- 18 = 2x2 – 24
- 18 + 24 = 2x2
6 = 2x2
3 = x2
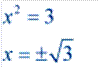
(ii)
2 (5) – 3(4) = x(5) – 2x(3)
10 – 12 = 5x – 6x
-2 = - x
x = 2
Question 8. If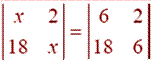 , then x is equal to
, then x is equal to
(A) 6 (B) ± 6 (C) – 6 (D) 0
Solution:
x(x) – 2(18) = 6(6) – 18(2)
X2 – 36 = 36 – 36
X2 = 36
x = ±6
Hence option B is correct
Question 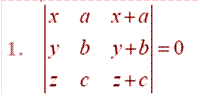
Answer:
Question 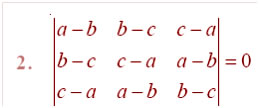
Answer:
Question 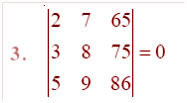
Answer:
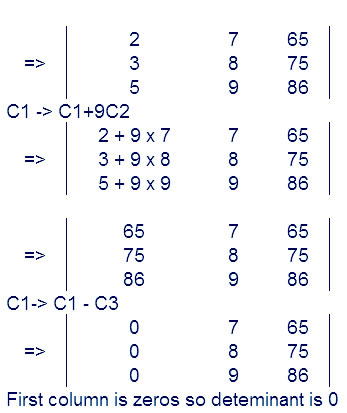
Question 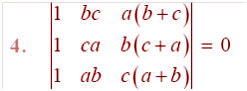
Answer:

Question 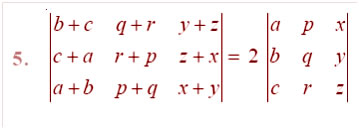
Answer:

Question 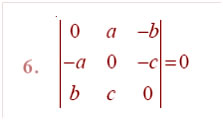
Answer:
 ]
]
Question 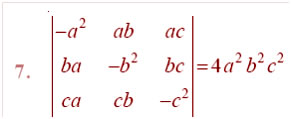
Answer:

Question 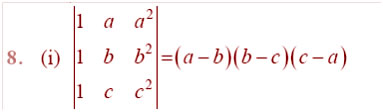
Answer:

Question 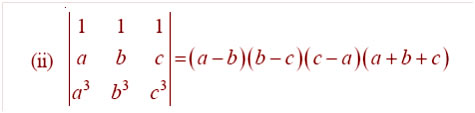
Answer:

=> (b-a)(c-a)(c2 –b2 + ac –ab +a2 –a2)
=> (b-a)(c-a){(c –b)(c+b) + a(c –b)}
=>(b-a)(c-a)(c-b)(a+b+c)
=> (a-b)(b-c)(c-a)(a+b+c)
Question 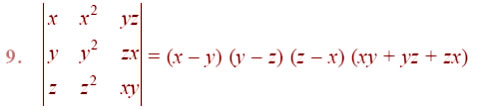
Answer:

Question 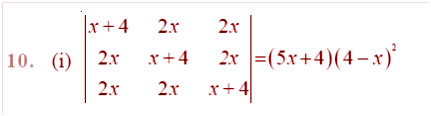
Answer:

Question 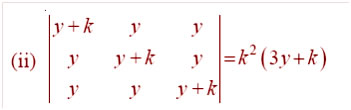
Answer:

Question 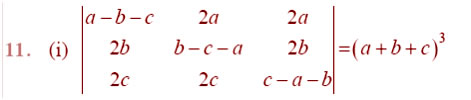
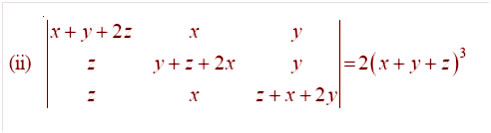
Answer:


Question 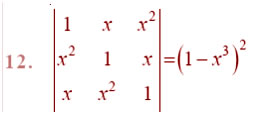
Answer:

Question 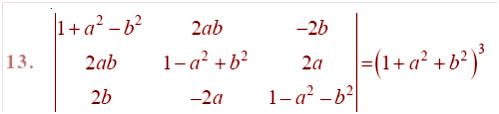
Answer:

Question 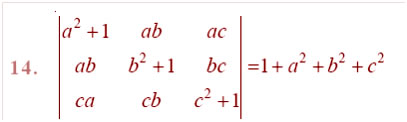
Answer:
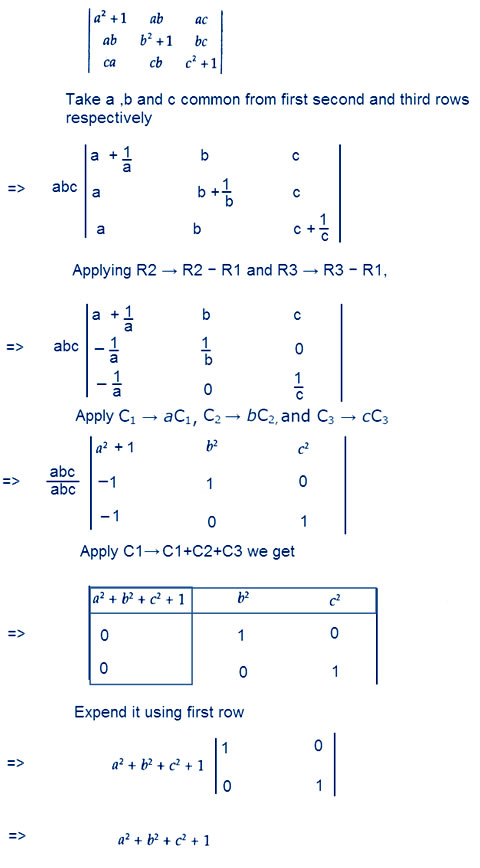
Question 15.Let A be a square matrix of order 3 × 3, then | kA| is equal to
(A) k| A| (B) k2 | A| (C) k3 | A| (D) 3k | A |
Answer:
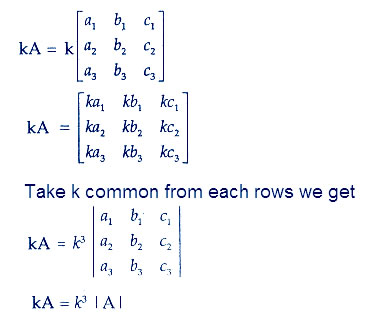
So option C is correct
Question 16. Which of the following is correct?
(A) Determinant is a square matrix.
(B) Determinant is a number associated to a matrix.
(C) Determinant is a number associated to a square matrix.
(D) None of these
Answer:We can calculate the determinant of a square matrix only so that Determinant is a number associated to a square matrix. Option (C) is correct
Question 1. Find area of the triangle with vertices at the point given in each of the following :
(i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8) (iii) (–2, –3), (3, 2), (–1, –8)
Answer:



Question 2. Show that points A (a, b + c), B (b, c + a), C (c, a + b) are collinear.
Answer:

Question 3. Find values of k if area of triangle is 4 sq. units and vertices are
(i) (k, 0), (4, 0), (0, 2) (ii) (–2, 0), (0, 4), (0, k)
Answer:

Answer is k = 0 and 8

Question 4.
(i) Find equation of line joining (1, 2) and (3, 6) using determinants.
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants.
Answer:


Question 5. If area of triangle is 35 sq units with vertices (2, – 6), (5, 4) and (k, 4). Then k is
(A) 12 (B) –2 (C) –12, –2 (D) 12, –2
Answer:
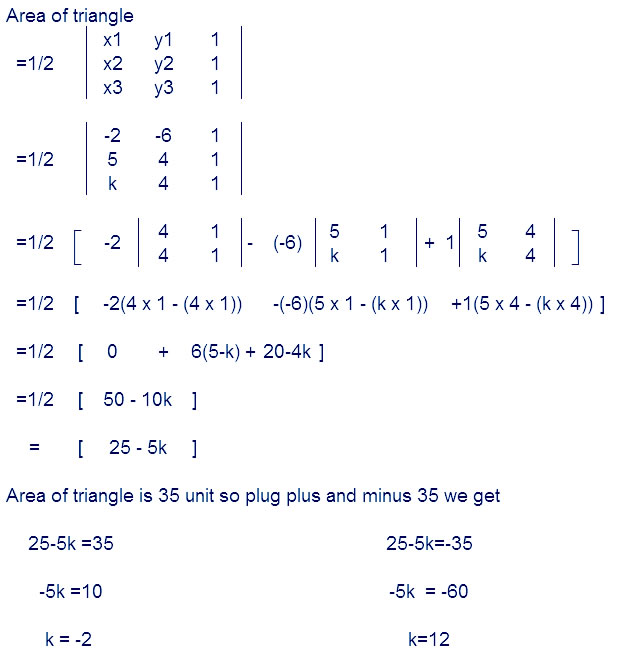
Question 
Answer:


Question 
Answer:
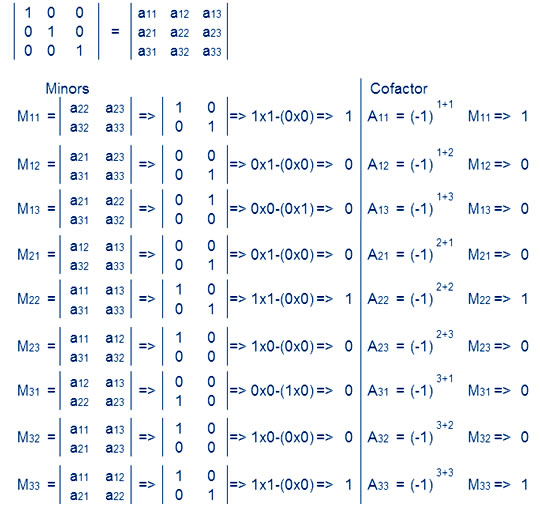
Answer part (ii)

Question 
Answer:

Question 
Answer:
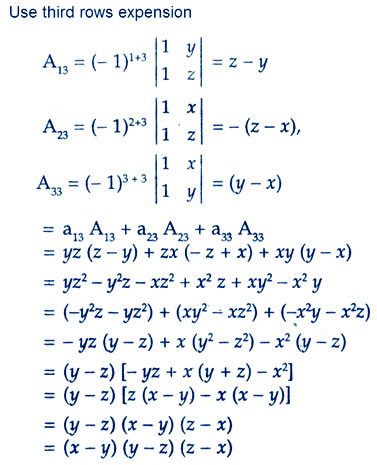
Question 
Answer:Value of determinant is always equal to sum of product of rows or columns with their corresponding cofactor
In option D there is first column operation
Question 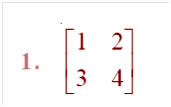
Answer:

Question 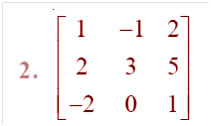
Answer:

Question 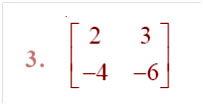
Answer:
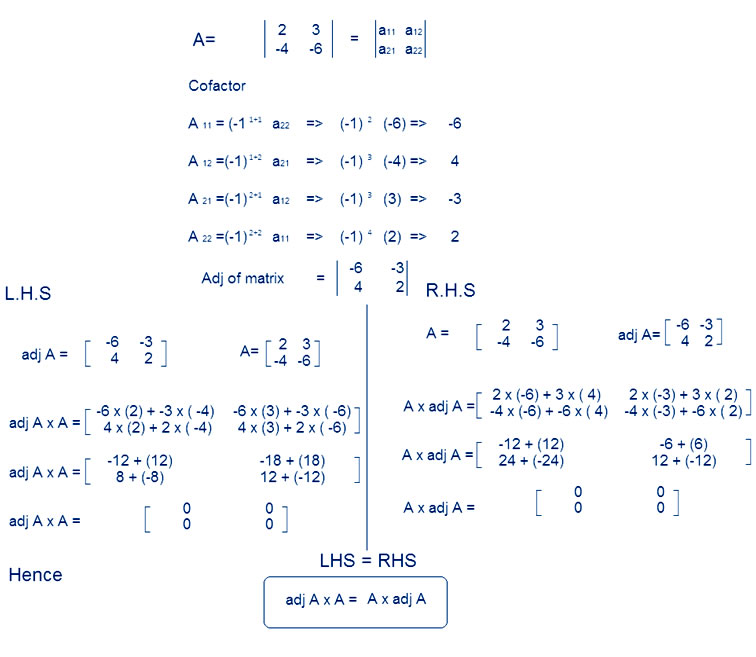
Question 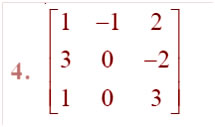
Answer:

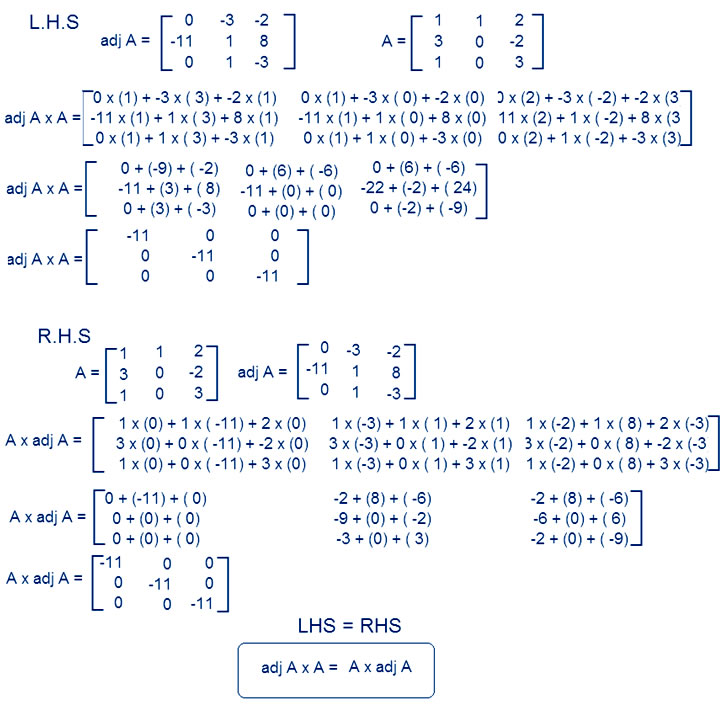
Question 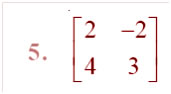
Answer:

Question 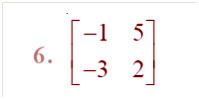
Answer:

Question 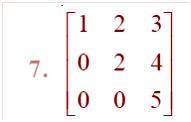
Answer:

Question 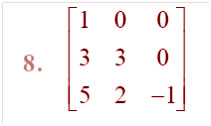
Answer:

Question 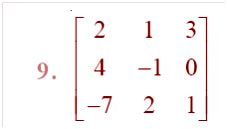
Answer:

Question 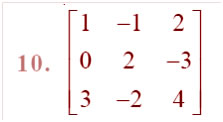
Answer:

Question 
Answer:

Question 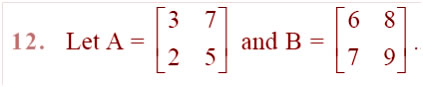 Verify that (AB)–1 = B–1 A–1.
Verify that (AB)–1 = B–1 A–1.
Answer:





Hence (AB)–1 = B–1 A–1
Question 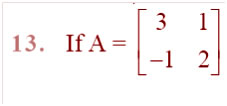 show that A2 – 5A + 7I = O. Hence find A–1.
show that A2 – 5A + 7I = O. Hence find A–1.
Answer:


Question 14. For the matrix 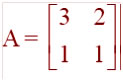 find the numbers a and b such that A2 + aA + bI = O.
find the numbers a and b such that A2 + aA + bI = O.
Answer:
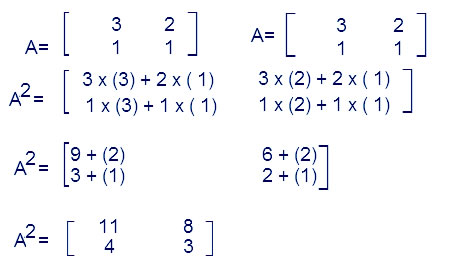


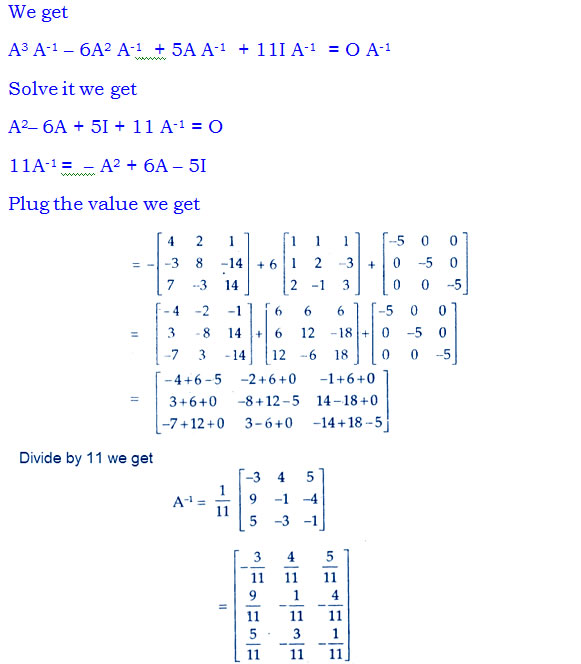
Question 15. For the matrix 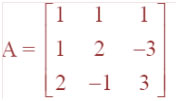 Show that A3– 6A2 + 5A + 11 I = O. Hence, find A–1.
Show that A3– 6A2 + 5A + 11 I = O. Hence, find A–1.
Answer:


Question 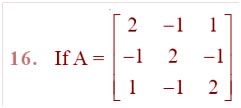
Answer:



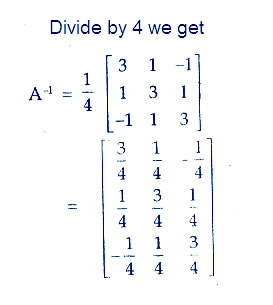
Question 17. Let A be a nonsingular square matrix of order 3 × 3. Then |adj A| is equal to
(A) |A| (B) |A|2 (C) |A|3 (D) 3|A|
Answer:We have the formula
Use property of determinant A.adj A = AI
Take mode both sides we get
|A.adj A| = |AI|
As A is matrix of 3x3 hence
|AI| = A3I
Hence
|A| |adj A| = |A|3
ide by |A| both side we get
|adj A| = |A2|
Hence option B is correct
Question 18. If A is an invertible matrix of order 2, then det (A–1) is equal to
(A) det (A) (B)1/det (A) (C) 1 (D) 0
Answer:We have the formula
AA-1 = I
Take determinant both side we get
|A ||A-1| = 1
Divide by |A| both side we get
|A-1| = 1/|A |
Hence option B is correct
Question 1. x + 2y = 2 and 2x + 3y = 3
Answer:
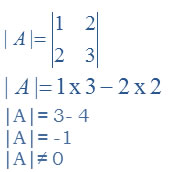
Equations has unique solutions. Hence equations are consistence
Question 2. 2x – y = 5 and x + y = 4
Answer:
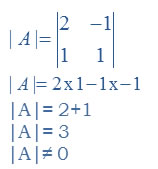
Equations has unique solutions. Hence equations are consistence
Question 3. x + 3y = 5 and 2x + 6y = 8
Answer:

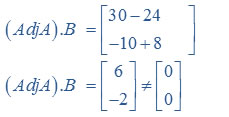
Hence equations are consistence
Question 4. x + y + z = 1 , 2x + 3y + 2z = 2 and ax + ay + 2az = 4
Answer:
Equation third is ided by a we get
x + y + z = 1
2x + 3y + 2z = 2
x + y + 2z = 4/a
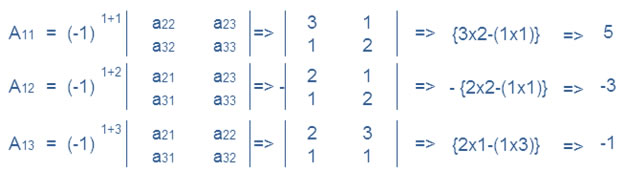
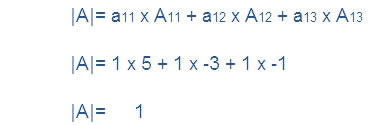
Hence |A| ≠0
So Equations has unique solutions. Hence equations are consistence
Question 3x–y – 2z = 2, 2y – z =-1 and –3x – 5y = 3
Answer:
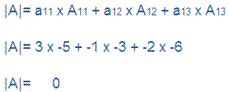
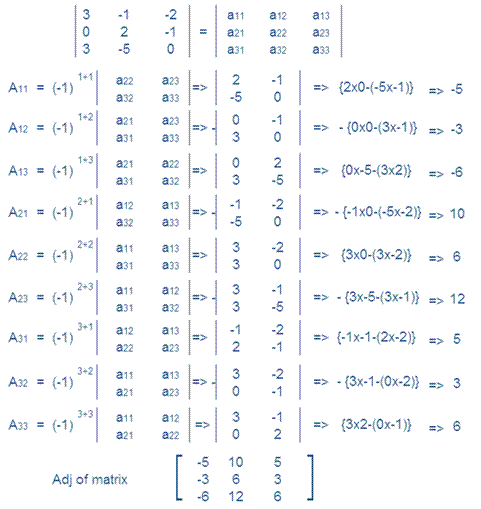
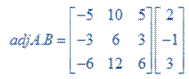
Multiply both matrices we get
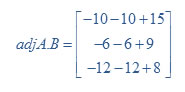
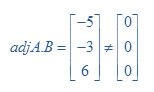
Hence it is inconsistence
Question 6. 5x – y + 4z = 5,2x + 3y + 5z = 2 and 5x – 2y + 6z = –1
Answer:
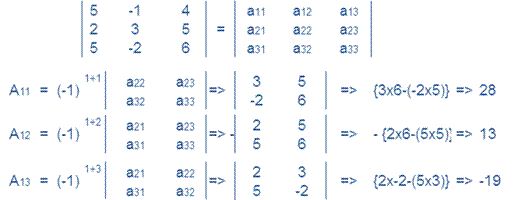
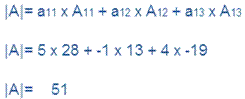
|A|≠0
Hence equations are consistence
Question 7. 5x + 2y = 4 and 7x + 3y = 5
Answer:

Hence answer is x =2 and y = -3
Question 8. 2x – y = –2 and 3x + 4y = 3
Answer:


Question 9. 4x – 3y = 3 and 3x – 5y = 7
Answer:
![]()

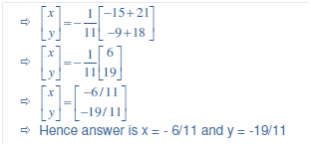
Question 10. 5x + 2y = 3 and 3x + 2y = 5
Answer:

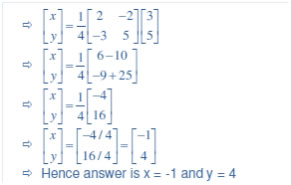
Question 11. 2x + y + z = 1, x – 2y – z =3/2 and 3y – 5z = 9
Answer:
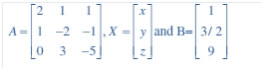


Question 12. x – y + z = 4, 2x + y – 3z = 0 and x + y + z = 2
Answer:
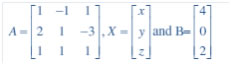


Question 13. 2x + 3y +3 z = 5, x – 2y + z = – 4 and 3x – y – 2z = 3
Answer:
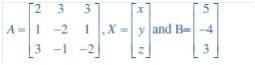


Question 14. x – y + 2z = 7,3x + 4y – 5z = – 5 and 2x – y + 3z = 12
Answer:
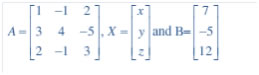


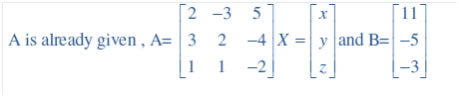
Question 15. If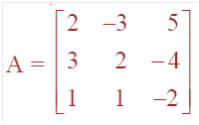 , find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y – 4z = – 5 x + y – 2z = – 3
, find A–1. Using A–1 solve the system of equations 2x – 3y + 5z = 11 3x + 2y – 4z = – 5 x + y – 2z = – 3
Answer:


Question 16. The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70. Find cost of each item per kg by matrix method.
Answer:
Let cost of each Kg of onion = Rs x
Cost of each Kg of wheat = Rs y
And cost of each Kg of rice = Rs z
Given that cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60
So
4x + 3y + 2 z = 60 …(1)
Given that The cost of 2 kg onion, 4 kg wheat and 6 kg rice is Rs 90
So
2x + 4y + 6z = 90
Divide equation by 2 we get
X + 2y + 3z = 45 … (2)
Given that The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70.
So
6x + 2y + 3z = 70 … (3)
So our set of equation is
4x + 3y + 2 z = 60
2x + 4y + 6z = 90
6x + 2y + 3z = 70
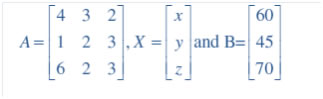


Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.