NCERT Solutions Class 12 Chemistry UNIT 1 THE SOLID STATE Exercise

Intext Questions Chapter 1 Class 12 Chemistry THE SOLID STATE Ncert Solutions

Question 1.1: Why are solids rigid?

Answer
Solids are rigid because the intermolecular forces of attraction that are present in solids are very strong. The constituent particles of solids cannot move from their positions they can only vibrate from their mean positive.

Question 1.2: Why do solids have a definite volume?

Answer
Solids have strong intermolecular forces of attraction. The constituent particles of solids cannot move from their positions they can only vibrate from their mean positive. That is why do solids have a definite volume.

Question 1.3: Classify the following as amorphous or crystalline solids: Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, olyvinylchloride, fibre glass, copper.

Answer

Polyurethane	Amorphous solids
Nnaphthalene	Crystalline solids
benzoic acid	Crystalline solids
Teflon	Amorphous solids
Potassium nitrate	Crystalline solids
Cellophane	Amorphous solids
Polyvinylchloride	Amorphous solids
Fibre glass	Amorphous solids
Copper	Crystalline solids

Question 1.4: Why is glass considered a super cooled liquid?

Answer
Glass is a amorphous solid so all amorphous solid have a tendency to flow, though very slowly. Hence, glass is considered as a super cooled liquid. That is why the glass windows and doors become slightly thicker at the bottom than at the top with the time.

Question 1.5: Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show cleavage property?

Answer
Isotropic solid has same value of reflective index in all the direction. All isotropic solid are amorphous solid.Amorphous solid cuts into two pieces with irregular surfaces Therefore,.Amorphous solid does not show the cleavage property.

Question 1.6: Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphide, graphite, rubidium, argon, silicon carbide.

Answer

Potassium sulphate	Ionic solid
Benzene	Molecular solid (non−polar)
Urea	Polar molecular solid
Ammonia	Polar molecular solid
Water	Hydrogen bonded molecular solid
Zinc sulphide	Ionic solid
Graphite	Covalent or network solid
Rubidium	Metallic solid
Argon	Non−polar molecular solid
Silicon carbide	Covalent or network solid

Question 1.7: Solid A is a very hard electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?

Answer
The given properties are the properties of a covalent or network solid. Therefore, the given solid is a covalent or network solid. Diamond and quartz (SiO₂) are the example of this types solid

Question 1.8: Ionic solids conduct electricity in molten state but not in solid state. Explain.

Answer
The constituent particles of ionic solid are not free to move in solid state. Therefore ionic solid are insulator in solid phase. Ions becomes free to move in molten state so ionic solid can conduct electricity in molten state.

Question 1.9: What type of solids are electrical conductors, malleable and ductile?

Answer
Metallic solids have these properties

Question 1.10: Give the significance of a ‘lattice point’.

Answer
Each lattice point represents one constituent particles of crystal. Particles of a solid may be an atom, a molecule, or an ion.

Question 1.11: Name the parameters that characterize a unit cell.

Answer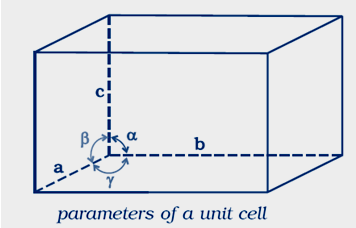
Following parameters characterized the unit cell.
(i) Three edges, a, b, and c. These edges may or may not be equal or mutually perpendicular.
(ii) Angles between the edges are represented by $/alpha ,/beta /text{ and }/gamma $. $/alpha ,/beta /text{ and }/gamma $are the opposite angle of side a, b and c respectively.

Question 1.12: Distinguish between
(i) Hexagonal and monoclinic unit cells
(ii) Face−centred and end−centred unit cells.

Answer

(i) Hexagonal unit cell
For a hexagonal unit cell,

Monoclinic unit cell
For a monoclinic cell,

(ii) Face−centred unit cell
A face−centred unit cell has one constituent particle which is present at each corner and one at the centre of each face.
End−centred unit cell
A end−centred unit cell has one particles at each corners and one at the centre of any
two opposite faces.

Question 1.13: Explain how much portion of an atom located at (i) corner and (ii) body−centre of a cubic unit cell is part of its neighboring unit cell.

Answer

(i)the atom of corner of a cubic unit cell is shared by eight adjacent unit cells.
Therefore, portion of the atom at the corner = 8 × 1/8 = 1 atom.

(ii) The atoms present at the center of the body is not shared by its neighboring unit cell.
Therefore, portion of the atom at the center = 1 atom

Question 1.14: What is the two dimensional coordination number of a molecule in square close packed layer?

Answer
In two dimensional square close−packed layer, a molecule touches four neighbor atoms. Therefore, 4 is the two dimensional coordination number of a molecule in square close packed layer

Question 1.15: A compound forms hexagonal close−packed structure. What is the total number of voids in 0.5 mol of it? How many of these are tetrahedral voids?

Answer
Number of atoms in close packaging = 0.5 mol
1 has 6.022 ×10²³ particles
So that
Number of close−packed particles
= 0.5 × 6.022 × 10²³ = 3.011 × 10²³
Number of tetrahedral voids = 2 × number of atoms in close packaging
Plug the values we get
Number of tetrahedral voids = 2 × 3.011 × 10²³
= 6.022 × 10²³
Number of octahedral voids = number of atoms in close packaging
So that
Number of octahedral voids = 3.011 × 10²³
Total number of voids = Tetrahedral void + octahedral void
= 6.022 × 10²³ + 3.011 × 10²³
= 9.03 × 10²³

Question 1.16: A compound is formed by two elements M and N. The element N forms ccp and atoms of M occupy 1/3rd of tetrahedral voids. What is the formula of the compound?

Answer
Let number of atoms of the element N = n
Number of tetrahedral voids = 2 × number of atoms in close packaging
Therefore
Number of tetrahedral voids = 2n
It is given that the atoms of element M occupy 1/3rd of tetrahedral voids.
So that the number of atoms of M is = (1/3) × 2n
=(2/3)n
Ratio of the number of atoms of M and N
< class="fontmath">$M:N=/frac{2n}{3}:n$

Multiply by 3 and ide by n we get
M:N = 2:3
Hence , the formula of the compound is M₂N₃.

Question 1.17: Which of the following lattices has the highest packing efficiency (i) simple cubic (ii) body−centred cubic and (iii) hexagonal close−packed lattice?

Answer
(i)In a simple cubic lattice the atoms are located only on the corners of the cube.
Let take edge length or side of the cube = a,
Let take radius of each particles = r
The relation between radius and edge a

a = 2r
The volume of the cubic unit cell = side³
= a³
= (2r)³
= 8r³
Number of atoms in unit cell = 8 × 1 /8
= 1
The volume of the occupied space = (4/3)πr³

(ii) In body centered cubic two atoms diagonally

Let take edge length or side of the cube = a,
Let take radius of each particles= r

The diagonal of a cube is always a√3
The relation between radius and edge a will
a√3 = 4r
ide by root 3 we get
a = 4r/√3
total number of atoms in body centered cubic
number of atoms at the corner = 8 × 1/8 = 1
number of atoms at the center= 1
total number of atoms= 2
The volume of the cubic unit cell = side³
= a³
= (4r/√3)³
The volume of the occupied space = (4/3)πr³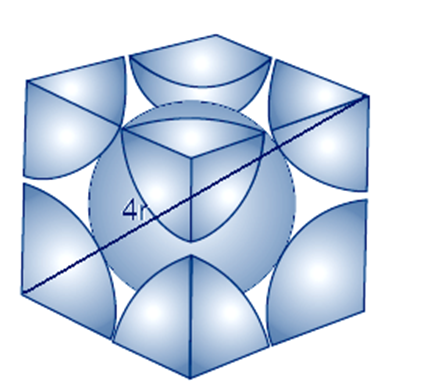

(iii) hexagonal close−packed lattice
Let take base of hexagonal is a and height is c
Each angle in hexagonal will 60 degree at base

Hexagonal close−packed lattice has the highest packing efficiency of 74%.

Question 1.18: An element with molar mass 2.7 × 10⁻² kg mol⁻¹ forms a cubic unit cell with edge length 405 pm. If its density is 2.7 × 10³ kg m⁻³, what is the nature of the cubic unit cell?

Answer
Given that
Density of element, p = 2.7 × 10³ kg m⁻³
Molar mass, M= 2.7 × 10⁻² kg mol⁻¹
Edge length, a= 405 pm
1 pm = 10⁻¹² meter
So edge in meter= 405 × 10⁻¹² m = 4.05 × 10⁻¹⁰ m
Let Z is the number of atoms in unit cell
Number of atoms in 1 mol of substance, NA = 6.022 × 10²³ atoms
Use formula
Density < class="fontmath">$p=/frac{ZM}{{{a}^{3}}{{N}_{A}}}$
Cross multiply we get
< pa³N_A= ZM
Divide by M we get < class="fontmath">/[Z=/frac{p{{a}^{3}}{{N}_{A}}}{M}/]
Now plug the values we get
< class="fontmath">$/Rightarrow Z=/frac{2.7x{{10}^{3}}(4.05x{{10}^{-10}})(6.022x{{10}^{23}})}{2.7x{{10}^{-2}}}$
< class="fontmath">$/Rightarrow Z=/frac{2.7x{{10}^{3}}(4.05x{{10}^{-10}})(6.022x{{10}^{23}})}{2.7x{{10}^{-2}}}$
Hence there are four atoms of the element are present per unit cell So that, this unit cell can a face−centred cubic (fcc) or cubic close−packed (ccp).

Question 1.19: What type of defect can arise when a solid is heated? Which physical property is effected by it and in what way?

Answer
On heating, some atoms or ions leave the lattice site completely so vacancy defect can arise. A solid will show vacancy defect when some of the lattice sites are vacant. Vacancy defect always decreases the density of the solid

Question 1.20: What type of stoichiometric defect is shown by:
(i) ZnS(ii) AgBr

Answer
(i) ZnS shows Frenkel defect.
(ii) AgBr shows Frenkel and Schottky defect both .

Question 1.21: Explain how vacancies are introduced in an ionic solid when a cation of higher valence is added as an impurity in it.

Answer
When a cation of higher valence is added as impurity in an ionic solid . two or more than two cations of lower valances is replace by less than 2 ions of higher valances . To maintain the electrical neutrality few sites become vacant.
For example,
Sr²⁺ is added to NaCl, each Sr²⁺ ion replaces two Na⁺ ions. Because the charge on 1 ions of Sr²⁺ is equal to charge on two ions of Na⁺. and One Na⁺ ions leave there site

Question 1.22: Ionic solids, which have anionic vacancies due to metal excess defect, develop colour.Explain with the help of a suitable example.

Answer
If ionic solid has metal excess defect due to anionic vacancies then ionic solid generate colur due to F –centers. Electrons absorb energy from the visible part of radiation and get excited.
For example, If the crystals of NaCl are heated in an atmosphere of sodium vapours, the sodium atoms deposited on the surface of the crystal .Chlorine ions comes outside the surface of crystal and react with this deposited sodium .Na atoms on the surface lose electrons to form Na+ ions and released electron occupy the vacant anionic sites. These electrons get excited by absorbing energy from the visible light falling on the crystal and generate yellow colour.

Question 1.23: A group 14 element is to be converted into n−type semiconductor by doping it with a suitable impurity. To which group should this impurity belong?

Answer
An n−type semiconductor conducts the electricity due to presence of extra electrons. So that, an element of group 14th can be converted to n−type semiconductor by doping it with the element of group 15 like P and As .

Question 1.24:What type of substances would make better permanent magnets, ferromagnetic or ferrimagnetic. Justify your Solution:.

Answer
Ferromagnetic substances would make better permanent magnets. A few substances like iron, cobalt, nickel, gadolinium and CrO2 are attracted very strongly by a magnetic field. Such substances are called ferromagnetic substances. Besides strong attractions, these substances can be permanently magnetized. In solid state, the metal ions of ferromagnetic substances are grouped together into small regions called domains. Thus, each domain acts as a tiny magnet. In an unmagnified piece of a ferromagnetic substance the domains are randomly oriented and their magnetic moments get cancelled. When the substance is placed in a magnetic field all the domains get oriented in the direction of the magnetic field (and a strong magnetic effect is produced. This ordering of domains persist even when the magnetic field is removed and the ferromagnetic substance becomes a permanent magnet.

Exercise Chapter 1 Class 12 Chemistry THE SOLID STATE Ncert Solutions

Question 1:Define the term amorphous. Give a few examples of amorphous solids.
Answer
Amorphous solids are the solids whose constituent particles have a completely random arrangement. Amorphous solids do not have a sharp melting point and melt over a range of temperature. These solids are isotropic in nature. Amorphous solid have elasticity, electric conductance, reflective index and rate of dissociation are the same throughout all the direction. Amorphous solid always flow very slowly therefore, amorphous solids are sometimes called pseudo solids or super cooled liquids. Amorphous solid do not have definite heat of fusion. When we cut a piece of amorphous solid cut with a sharp–edged tool, they cut into two pieces with irregular surfaces.
Examples :– glass, rubber, and plastic. Question 2. What makes a glass different from a solid such as quartz?
Answer: Under what conditions could quartz be converted into glass? Glass is a super cool liquid .glass is an amorphous solid. Glass has short range order .In below figure we can see that Quartz has long range order while glass does not have long range order.

To convert quartz in to glass melt the quartz and cool it rapidly, quartz will be converted in to glass Question 3. Classify each of the following solids as ionic, metallic, molecular, network (covalent) or amorphous.
Answer:

(i) Tetra phosphorus decoxide (P4O10)	Molecular
(ii) Ammonium phosphate (NH4)3PO4	Ionic
(iii) SiC	Network (covalent)
(iv) I2	Molecular
(v) P4	Molecular
(vi) Plastic.	Amorphous
(vii) Graphite	Network (covalent)
(viii) Brass	Metallic
(ix) Rb	Metallic
(x) LiBr	Ionic
(xi) Si	Network (covalent)

Question 4. (i) What is meant by the term coordination number ?
(ii) What is the coordination number of atoms
(a) in a cubic close packed structure?
(b) in a body–centered cubic structure?
Answer:
(i) The coordination number of an atom, ion or molecule is the number of constituent particles which touch that particular atom, atom or molecule.
(ii)
(a) in a cubic close packed structure coordination number is 12
(b) ) in a body–centered cubic structure coordination number is 8.
Question 5. How can you determine the atomic mass of an unknown metal if you know its density?
Answer:
Let consider a cubic crystal:
Let take volume of a unit cell = a³
Number of atoms in unit cell = z
Mass of each single atom = m
Molar mass of metal =M
Avogadro number =N_A
Use formula
Mass of the unit cell = number of atoms in unit cell × mass of each atom = z × m …(1)
Mass of each atom(m) = Molar mass / Avogadro number
Plug the value of m in equation (1) we get
Mass of unit cell =zM /N_A … (2)
Density of the unit cell = mass of unit cell / volume of unit cell

Using above formula we can calculate the atomic mass of unknown metal
Question 6. Stability of a crystal is reflected in the magnitude of its melting points. Comment.
Collect melting points of solid water, ethyl alcohol, diethyl ether and methane from a data book. What can you say about the intermolecular forces between these molecules?
Answer:
Melting points of substances
Water = 273K
Ethyl alcohol = 155•7K
Diethyl ether = 156•8K
Methane = 90•5K.
The stability of crystals depends up on the packing of the atoms. if there are strong force of attraction between the constituent particles then greater the stability.
Water – strong intermolecular hydrogen bonding
Ethyl alcohol – strong intermolecular hydrogen bonding.
Diethyl ether – it is a polar molecule so there is dipole –dipole attraction
Methane – is a non–polar molecule so that there is weak van der Waals forces (London dispersion forces).

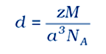
Question 7. How will you distinguish between the following pairs of terms
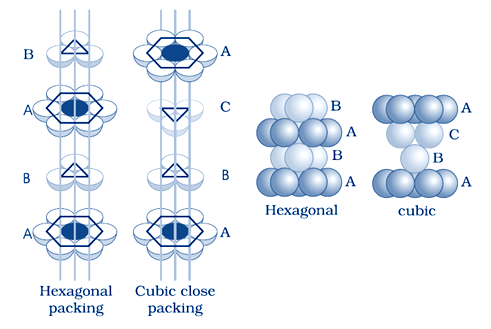
(i) Hexagonal close packing and cubic close packing
(ii) Crystal lattice and unit cell
(iii) Tetrahedral void and octahedral void.

Answer: (i)
Hexagonal close packing:–
when the tetrahedral voids of the second layer is covered by the spheres of the third layer. so that the spheres of the third layer are exactly aligned with those of the first layer, we get a pattern of spheres which is repeated in alternate layers. This pattern can be written in the form of ABAB ....... pattern. This structure is called hexagonal close packed (hcp) structure. Magnesium and zinc metals have this pattern

cubic close packing:– When the third layer is placed above the second layer in a manner such that its spheres cover the octahedral voids. and the spheres of the third layer are not aligned with first or the second layer, arrangement is called “C’ type.This pattern of layers is often written as ABCABC ........... This structure is called cubic close packed (ccp)

(ii)Crystal lattice :–
If the constituent particles are represented by dot (.) ,The periodic and systematic arrangement of these dots in three dimensions is called Crystal lattice.
Or
If each particle in three dimensional arrangement of constituent particles in a crystal is represented by a point, the arrangement is called crystal lattice. Thus, a regular three dimensional arrangement of constituent particles which represented by points in space is called a crystal lattice.

Unit cell :– the smallest repeating unit in space lattice is called unit cell. When we repeat unit cell in all dimensions, we get a structure of the crystal. Properties of unit cell are measured by length of edges and the angles between the edges.

(iii) Tetra hendral void :–
When a sphere of second layer is touching three sphere of first layer and the centers of all four sphere are at the corners of tetrahedron, the empty space which has tetra hendral arrangement is called tetra hedral void.
Octahedral void :–
When the tetrahedral void are formed at the corners of six sphere, each octa hedral void generate two set of equilateral triangles which are opposite to each other are called octahedral voids

Question 8 How many lattice points are there in one unit cell of each of the following lattice?
(i) Face–centred cubic
(ii) Face–centred tetragonal
(iii) Body–centred

Answer:
(i) Face–centred cubic:-
A face–centred cubic (fcc) unit cell contains atoms at all the corners and at the centre of all the faces of the cube.

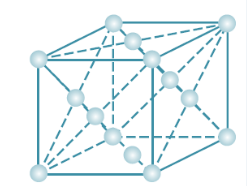
So lattice point at the corner = 8
Lattice point at the center of all faces = 6
Total number of lattice point = 14

(ii) Face–centred tetragonal
lattice point at the corner = 8
Lattice point at the center of all faces = 6
Total number of lattice point = 14

(iii) Body–centred
In Body centered cubic there are 8 lattice point at the corner and 1 is at the center so total 8+1 =9 lattice point

Question 9. Explain
(i) The basis of similarities and differences between metallic and ionic crystals.
(ii) Ionic solids are hard and brittle.

Answer
(i) The constituent particles of both metallic and ionic crystals are held by strong electrostatic force of attraction. In metals there is strong force of attraction between the mobile electron and positively change ions. In ionic crystals there are strong force of attraction between anion and cation. As both types of crystals have strong force of attraction so there melting and boiling points are high. Metal have free mobile electron so they conduct electricity in all there phase while ionic compound conduct electricity at molten or aqueous state only.

(ii) The constituent particles of ionic compound are held by strong electrostatic force of attraction. In ionic crystals there are strong force of attraction between oppositely changed anions and cations. As the electrostatic force of attraction is very strong so that the charged ions are held in fixed positions and they cannot move easily . This is the reason of ionic crystals to be hard and brittle.

Question 10 Calculate the efficiency of packing in case of a metal crystal for
(i) simple cubic
(ii) body–centred cubic
(iii) face–centred cubic (with the assumptions that atoms are touching each other).

Answer
(i)
In a simple cubic lattice the atoms are located only on the corners of the cube.
Let take edge length or side of the cube = a,
Let take radius of each particles= r
The relation between radius and edge a
a = 2r
The volume of the cubic unit cell = side³
= a³
= (2r)³
= 8r³
Number of atoms in unit cell = 8 x 1 /8
= 1
The volume of the occupied space = (4/3)πr³

(ii)In body centered cubic two atoms diagonally

Let take edge length or side of the cube = a,
Let take radius of each particles= r
The diagonal of a cube is always a√3
The relation between radius and edge a will
a√3 = 4r
ide by root 3 we get
a= 4r/√3
total number of atoms in body centered cubic
number of atoms at the corner = 8 x 1/8 = 1
number of atoms at the center = 1
total number of atoms= 2
The volume of the cubic unit cell = side³
= a³
= (4r/√3)³
The volume of the occupied space = (4/3)πr³

(iii)
Let take edge length or side of the cube = a
Let take radius of each particles= r
The diagonal of a square is always a√2
The relation between radius and edge a will
a√2 = 4r
ide by root 3 we get
a= 4r/√2
total number of atoms in body centered cubic
number of atoms at the corner = 8 x 1/8 = 1
number of atoms at the face = 6 x 1/2 = 3
total number of atoms= 4
The volume of the cubic unit cell = side³
= a³
= (4r/√2)³
= (2√2 r)³
The volume of the occupied space = (4/3)πr³

Question 11 Silver crystallises in fcc lattice. If edge length of the cell is 4.07 × 10^-8 cm and density is 0.5 g cm³, calculate the atomic mass of silver.

Answer
Edge of length of cell a = 4.07x10^-8cm
Density p = 10.5 g /cm³
Number of atoms in unit cell of fcc lattice = 4
Avogadro number NA = 6.022x10²³
Use formula
Density$p = /frac{{ZM}}{{{a^3}{N_A}}}$
Cross multiply we get
ZM = pa³N_A
Divide by Z we get
/[M = /frac{{p{a^3}{N_A}}}{Z}/]
Plug the value we get
/[M=/frac{10.5{{(4.07)}^{3}}6.022x{{10}^{23}}}{4}/]
/[M = /frac{{10.5x67.41x6.022}}{4}/]
/[M = 107.09g{/rm{ }}mo{l^{ - 1}}/]

Question 12 A cubic solid is made of two elements P and Q. Atoms of Q are at the corners of the cube and P at the body–centre. What is the formula of the compound? What are the coordination numbers of P and Q?

Answer
Number of atoms at corner in cubic solid = 1/8 x 8 = 1
Number of atoms at the center in BCC= 1
Hence the formulas of compound will PQ

Question 13 Niobium crystallises in body–centred cubic structure. If density is 8.55 g cm^–3, calculate atomic radius of niobium using its atomic mass 93 u.

Answer Edge of length of cell a = ?
Density p = 8.55 g /cm³
Number of atoms in unit cell of BCC lattice Z = 2
Avogadro number NA = 6.022x10²³
Use formula
Density $p=/frac{ZM}{{{a}^{3}}{{N}_{A}}}$
Cross multiply we get
pa³N_A= ZM

Divide by PN_A we get
/[{{a}^{3}}=/frac{MZ}{p{{N}_{A}}}/]
Plug the values we get
/[{{a}^{3}}=/frac{93x2}{8.55x6.022x{{10}^{23}}}c{{m}^{3}}/]
/[{{a}^{3}}=3.61x{{10}^{-23}}c{{m}^{3}}/]
Take cube root both side we get
/[a={{/left( 3.61x{{10}^{-23}} /right)}^{1/3}}cm/]
/[a={{/left( 36.1x{{10}^{-24}} /right)}^{1/3}}c{{m}^{{}}}/]
/[a=/left( 36.1{{)}^{1/3}}x({{10}^{-24/3}}) /right)c{{m}^{{}}}/]
/[a=/left( 3.30x{{10}^{-8}} /right)c{{m}^{{}}}/]
For BCC
$r=/frac{a/sqrt{3}}{4}$
Plug the value of a we get
$r=/frac{3.30x{{10}^{-8}}x1.732}{4}cm$
$r=1.43x{{10}^{-8}}cm$

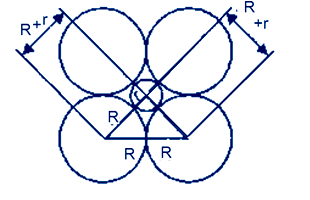
Question 14 If the radius of the octahedral void is r and radius of the atoms in closepacking is R, derive relation between r and R.

AnswerLet take r and R are the radii of the octahedral site and atoms respectively,then use Pythagoras theorem we get
(2R)² = (R+r)² +(R+r)²
4R² = 2(R+r)²
Divide by 2 we get
2R² = (R+r)²
Take root both side we get
R√2 =R+r
R√2 – R = r
r = R(√2–1)
value of √2= 1.414
r = R(1.414–1)
r = 0.414 R

Question 15 Copper crystallises into a fcc lattice with edge length 3.61 × 10^–8 cm. Show that the calculated density is in agreement with its measured value of 8.92 g cm^-3.

AnswerGiven that
Length of edge, a = 3.61x10^–8 cm
Atomic mass of cupper, M = 63.55 g/mol
Avogadro constant, NA = 6.022x10²³ per mol
Number of atoms in unit cell of FCC, Z= 4
Use formula of density

$p=/frac{ZM}{{{a}^{3}}{{N}_{A}}}$
Plug the values in this formula we get
< class="fontmath">$p=/frac{4x63.55}{{{(3.61x{{10}^{-8}})}^{3}}(6.022x{{10}^{23}})}/frac{g}{c{{m}^{3}}}$
$p=/frac{254.2}{(47.04x{{10}^{-24}})(6.022x{{10}^{23}})}/frac{g}{c{{m}^{3}}}$
$p=/frac{254.2}{28.318}/frac{g}{c{{m}^{3}}}$
$p=8.92/frac{g}{c{{m}^{3}}}$

Question 16 Analysis shows that nickel oxide has the formula Ni_0.98O_1.00. What fractions of nickel exist as Ni²⁺ and Ni³⁺ ions?

AnswerFormula is Ni_0.98O_1.00
So the ration of Ni : O = 98:100
So if there are 100 atoms of oxygen then 98 atoms of Ni
Let number of atoms of Ni⁺² = x
Then number of atoms of Ni⁺³ = 98–x
Charge on Ni = charge on O
So that oxygen has charge –2
3(98–x) + 2x = 2 (100)
294 –3x +2x = 200
–x = – 94
x = 94
Percentage of Ni⁺² = (atom of Ni⁺²/total number of atoms of Ni)100
=100(94/98)*100
= 96%
Percentage of Ni⁺³
=100 – Ni⁺²
=100 – 96
= 4 %

Question 17 What is a semiconductor? Describe the two main types of semiconductors and contrast their conduction mechanism.

AnswerSemiconductors allow to flow a very small quantity of electric current through them at the room temperature. These are the solids with conductivities in the intermediate range from 10^–6 to 10⁴ ohm^–1m^–1.Semiconductors are perfect insulator at absolute zero. Silicon and Germanium are examples of semiconductor.
There are two types of main semiconductors
(i) n–type semiconductor (ii) p–type semiconductor

(i) n–type semiconductor:
there semiconductors have Electron – rich impurities. Silicon and germanium belong to group 14 of the periodic table and each has four valence electrons . Four out of five electrons are used in the formation of four covalent bonds with the four neighbouring silicon atoms. Extra fifth electron is becomes delocalized. These delocalized electrons increase the conductivity of doped silicon or germanium both . Here the increase in conductivity is due to the negatively charged mobile electron. Hence semiconductors doped with electron–rich impurity are called n–type semiconductor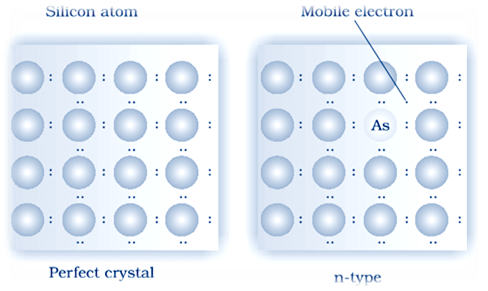


(ii) p–type semiconductor: Si or Ge can also be doped with a group 13 element. The elements of group 13 contains only three valence electrons. Elements of 14th group have has 4 valence electron. The place where the fourth valence electron is missing is called electron hole .An electron from a neighbouring atom can come and fill the electron hole, but in doing so it would leave an electron hole at its original position. If it happens, it would appear as if the electron hole has moved in the direction opposite to that of the electron that filled it. Under the influence of electric field, electrons would move towards the positively charged plate through electronic holes, but it would appear as if electron holes are positively charged and are moving towards negatively charged plate. This type of semi conductors are called p–type semiconductors.

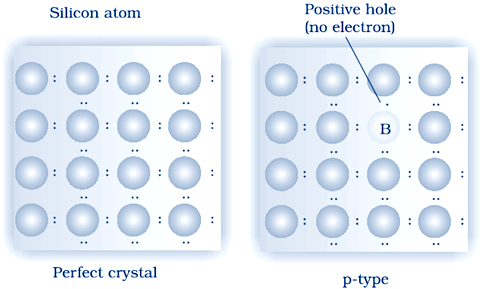
Question 18: Non–stoichiometric cuprous oxide, Cu₂O can be prepared in laboratory. In this oxide, copper to oxygen ratio is slightly less than 2:1. Can you account for the fact that this substance is a p–type semiconductor?

Answer The charge on Cu will +1 in Cu₂O and in normal compound Cu has + 2 charge . and every 2 ions of Cu +1 will replaced by one ion of Cu +2. The conductance is arise due to these positive holes hence it will form a p type of semiconductor.

Question 19: Ferric oxide crystallises in a hexagonal close–packed array of oxide ions with two out of every three octahedral holes occupied by ferric ions. Derive the formula of the ferric oxide.

Answer Suppose the number of oxide (O^2–) ions = N.
Number of octahedral void = number of anions
So that the number of octahedral voids = N
Given that
Two out of every three octahedral holes are occupied by ferric ions.
So that the number of ferric (Fe³⁺) ions = 2N/3
The ratio of the number of Fe³⁺ ions to the number of O²⁻ ions,
Fe³⁺ : O²⁻ = 2N/3 : N
Multiply 3 and ide by N we get
Fe³⁺ : O²⁻ = 2 : 3
Hence, the formula of the ferric oxide is Fe₂O₃.

Question 20: Classify each of the following as being either a p–type or an n–type semiconductor:
(i) Ge doped with In(ii) B doped with Si.

Answer
(i) Ge is a 14^th group element and In is a 13^th group element .When 14^th group element is doped with In a 13^th group element, a electron deficit hole created .Hence Ge doped with In will generate p–type semiconductor.

(ii)B is a ^13th group element and Si is a 14^th group element .When 13^th group element is doped with In a 14^th group element, created hole will generate n–type semiconductor.

Question 21: Gold (atomic radius = 0.144 nm) crystallises in a face–centred unit cell. What is the length of a side of the cell?

Answer
Given that
Radius of atom R= 0.144 nm
For a face–centered unit cell
Edge a = 2√2 R
Plug the values we get
Edge a= 0.144 x 2 x 1,414 nm
Edge a= 0.407 nm
Solution:– The length of a side of the cell = 0.407 nm

Question 22: In terms of band theory, what is the difference
(i) Between a conductor and an insulator
(ii) Between a conductor and a semiconductor

Answer (i)
A conductor may conduct electricity due to movement of electrons or ions. If valance band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily flow under an applied electric field and the metal shows conductivity.
If the gap between filled valence band and the next higher unoccupied band (conduction band) is large, electrons cannot jump to it and such a substance has very small conductivity and it behaves as an insulator .


(ii)
A conductor may conduct electricity due to movement of electrons or ions. If valance band is partially filled or it overlaps with a higher energy unoccupied conduction band, then electrons can flow easily flow under an applied electric field and the metal shows conductivity.
In case of semiconductors, the gap between the valence band and conduction band is small. Therefore, some electrons may jump to conduction band and show some conductivity. Electrical conductivity of semi conductors increases with rise in temperature because with the rise of temperature more electrons can jump to the conduction band. Substances like silicon and germanium show this type of behaviour and are called semiconductors

Question 23: Explain the following terms with suitable examples:
(i) Schottky defect
(ii) Frenkel defect
(iii) Interstitials and
(iv) F–centres

Answer (i) Schottky Defect:
It is basically a vacancy defect in ionic solids. In order to maintain electrical neutrality, the number of missing cations and anions are equal. Like simple vacancy defect, Schottky defect also decreases the density of the substance. Number of such defects in ionic solids is quite significant.

(ii)Frenkel Defect:
This defect is shown by ionic solids. In this defect the smaller ions are dislocated from its normal site to an interstitial site . It generate a vacancy defect at its original site and an interstitial defect at itsnew location. Frenkel defect is also called dislocation defect.
In this type of defect, density remains same. Frenkel defect is shown by ionic substance in which there is a large difference in the size of ions, for example, ZnS, AgCl, AgBr and AgI shows this effect due to small size of Zn²⁺ and Ag⁺ ions.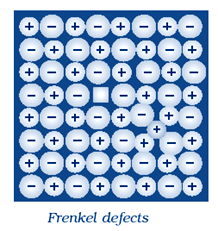

For example, in NaCl there are approximately 106 Schottky pairs per cm3 at room temperature. In 1 cm3 there are about 1022 ions. Thus, there is one Schottky defect per 1016 ions. Schottky defect is shown by ionic substances in which the cation and anion are of almost similar sizes. For example, NaCl, KCl, CsCl and AgBr. It may be noted that AgBr shows both, Frenkel as well as Schottky defects.

(iii) Interstitial Defect:
When some constituent particles(atoms or molecules) occupy an interstitial site,the crystal is said to have interstitial defect. This defect increases the density of the substance.Vacancy and interstitial defects as explained above can be shown by non–ionic solids. Ionic solids must always maintain electrical neutrality.Rather than simple vacancy or interstitial defects, they show these defects as Frenkel and Schottky defects.

(iv) F–centres:
A compound may have excess metal ion. When negative ion is absent from its lattice side and compound have excess metal ion and leaving a hole which occupied by electron to maintain electrical neutrality , the ionic sites are called F center .Colour in these crystals are impart by unpaired electrons
These types of defects are found in crystals which have electric neutrality and Schoottky defects .The hole occupied by electron is called F–center. This F center is responsible for most of the interstitial properties of compound
For example We observe this effect when Crystals of NaCl heated in an atmosphere of sodium vapour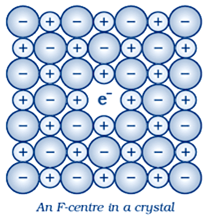

Question 24: Aluminium crystallises in a cubic close–packed structure. Its metallic radius is 125 pm.
(i) What is the length of the side of the unit cell?
(ii) How many unit cells are there in 1.00 cm³ of aluminum?

Answer
For the cubic close–packed structureLet a is the edge of the cube and r is the radius of atom
Given that r = 125 pm
a = 2√2 r
Plug the value of r we get
= 2 x 1.414 x125 pm
= 354 pm (approximately)
Volume of one unit cell = side³ = (354 pm)³
1 pm = 10^–10 cm
= (354 x 10^–10 cm)³
= (3.54 x 10^–8 cm)³
= 44.36 x 10^–24 cm³
= 4.4 × 10⁻²³ cm³
Total number of unit cells in 1.00 cm³
= total volume / size of each cell
= (1.00cm³)/( 4.4 × 10⁻²³ cm³)
= 2.27 × 1022 unit cell

Question 25: If NaCl is doped with 10⁻³ mol % of SrCl₂, what is the concentration of cation vacancies?

Answer
Given Conetration of SrCl₂= 10⁻³ mol%
Concentration is in percentage so that take total 100 mol of solution
Number of moles of NaCl = 100 – moles of SrCl₂
Moles of SrCl₂is very negligible as compare to total moles so
Number of moles of NaCl = 100
1 mol of NaCl is dipped with = 10−3/100 moles of SrCl₂
= 10^–5 mol of SrCl₂
So cation vacancies per mole of NaCl =10^–5 mol
1 mol = 6.022 x10²³ particles
So
So cation vacancies per mole of NaCl = 10–5 x 6.022 x10²³
= 6.02 x10¹⁸
So that, the concentration of cation vacancies created by SrCl₂is 6.022 × 10⁸ per mol of NaCl.

Question 26: Explain the following with suitable examples:
(i) Ferromagnetism
(ii)Paramagnetism
(iii)Ferrimagnetism
(iv)Antiferromagnetism
(v)12–16 and 13–15 group compounds.

Answer
(i) Ferromagnetism:–
Ferromagnetism: few substances like iron, cobalt, nickel, gadolinium and CrO2 are strongly attracted by a magnetic field. Such substances are known as ferromagnetic substances. These substances can be permanently magnetised with the help of strong electrostatic field. The metal ions of ferromagnetic substances are grouped together into small regions called domains in solid state. So that each domain acts as a tiny magnet. The domains of un magnetized piece of a ferromagnetic are randomly oriented so that their magnetic moments get cancelled out. When such substance is placed in a magnetic field, all the domains get oriented in the direction of the magnetic field and a strong magnetic effect is produced. This ordering of domains remains same even when the magnetic field is removed and the ferromagnetic substance becomes a permanent magnet.

(ii) Paramagnetism :–
few substances like O₂, Cu²⁺, Fe³⁺, Cr³⁺ are weekly attracted by a magnetic field.
These substabces are magnetised in a magnetic field in the same direction. When we remove magnetic field ,they lose their magnetism. paramagnetism is takes place due to presence of one or more unpaired electrons. These unpaired electron are attracted by the magnetic field.

(iii)Ferrimagnetism:
This effect is observed when the magnetic moments of the domains in the substance are aligned in parallel and anti–parallel directions in unequal numbers. Ferrimagnetic substances are weakly attracted by magnetic field as compared to ferromagnetic substances. Magnetite like Fe₃O₄ and ferrites like MgFe₂O₄ and ZnFe₂O₄ are examples

of such substances. On heating these substances lose their ferrimagnetism and become paramagnetic.

(IV)Antiferromagnetism:
Antiferromagnetic substances have domain structure similar to ferromagnetic substance. The domains of antiferromagnetic substance are oppositely oriented and cancel out each others magnetic moment . Example MnO is a Antiferromagnetic substance.

(V)12–16 and 13–15 group compounds.
The compounds of 12–16 group are prepared by combining elements of group 12 and group 16. While the compound of 13–15 group compounds are prepared by combining elements of group 13 and group15. These compounds are covalent and there ionicity depends up the difference in electro negativities of elements which involve in forming of these compounds. These compounds have special electrical and optical properties so that these compounds are used in industries for a variety of applications
Examples
ZnS, CdS ,CdSe and HgTe are example of 12–16 group compounds
InSb, AIP and GaAs are the example of 13–15 group compounds

Ncert Solution for class 6 to 12 download in pdf