
Ncert Solutions for class 11 subject Maths Chapter 10 Straight Linesin pdf Best Free NCERT Solutions for class 1 to 12 in pdf NCERT Solutions, cbse board, Maths, ncert Solutions for Class 11 Maths, class 11 Maths ncert solutions, Straight Lines, Class 11, ncert solutions chapter 10 Straight Lines, class 11 Maths, class 11 Maths ncert solutions, Maths ncert solutions class 11, Ncert Solutions Class 11 Mathematics Chapter 10 Straight Lines
Explanation of formula of class 11 mathematics chapter 10 straight line distance formula, section formula , midpoint formula, area of triangle when 3 coordinate points are given
Question 1: Draw a quadrilateral in the Cartesian plane, whose vertices are (–4, 5), (0, 7), (5, –5) and (–4, –2). Also, find its area.
Answer
Draw a Quadrilateral ABCD whose vertices are A (–4, 5), B (0, 7), C (5, –5), and D (–4, –2).
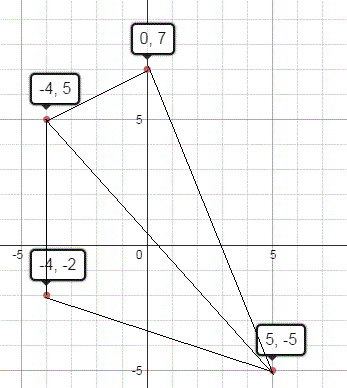
Area of quadrilateral ABCD = area of ∆ABC + area of ∆ACD
Relate the coordinate of ∆ ABC, A (–4, 5), B (0, 7), C (5, –5) with (x1, y1), (x2, y2), and (x3, y3) and use formula
\[ = \frac{1}{2}|{x_1}({y_2} - {y_3}+{x_2}({y_3} –{y_1} )+ +{x_3}({y_1} –{y_2} |\]
Plug the values, we get
=1/2|-4(7+5) + 0(-5 ,-5) + 5(5-7)|
=1/2|-4(12 +0 + 5(-2)|
=1/2|-48 -10|
=1/2 (58)
=29 unit2
Relate the coordinate of ∆ ABC, A (–4, 5), C (5, –5) and D (–4, –2). with (x1, y1), (x2, y2), and (x3,y3) and use formula
\[ = \frac{1}{2}|{x_1}({y_2} - {y_3}+{x_2}({y_3} –{y_1} )+ +{x_3}({y_1} –{y_2} |\]
Area of ∆ACD
=1/2|-4(-5+ 2) +5(-2-5) + (-4)(5 +5)|
= ½ |-4(-3) +5(-7) +(-4)(10)|
=1/2|12 -35 -40|
=1/2|-63|
= 63/2 unit2
Total area of quadrilateral (ABCD) = 29+ 63/2 = 121/2 unit2

3. Find the distance between P (x1, y1 and Q (x2, y2) when : (i) PQ is parallel to they-axis, (ii) PQ is parallel to the x-axis.
4. Find a point on the x-axis, which is equidistant from the points (7, 6) and (3, 4).
5. Find the slope of a line, which passes through the origin, and the mid-point of the line segment joining the points P (0, – 4) and B (8, 0).
6. Without using the Pythagoras theorem, show that the points (4, 4), (3, 5) and (–1, –1) are the vertices of a right angled triangle.
7. Find the slope of the line, which makes an angle of 30° with the positive direction of y-axis measured anticlockwise.
8. Find the value of x for which the points (x, – 1), (2,1) and (4, 5) are collinear.
9. Without using distance formula, show that points (– 2, – 1), (4, 0), (3, 3) and (–3, 2) are the vertices of a parallelogram.
10. Find the angle between the x-axis and the line joining the points (3,–1) and (4,–2).
11. The slope of a line is double of the slope of another line. If tangent of the angle between them is 1/3, find the slopes of the lines.
12. A line passes through (x1, y1) and (h, k). If slope of the line is m, show that k – y1 = m (h – x1).
13. If three points (h, 0), (a, b) and (0, k) lie on a line, show that a/h + b/k = 0
14. Consider the following population and year graph (Fig 10.10), find the slope of the line AB and using it, find what will be the population in the year 2010?
Question 1-3 (1)Write the equations for the x-and y-axes. (2) Passing through the point (– 4, 3) with slope 1/2 (3) Passing through (0, 0) with slope m.
please send your mail at ncerthelp@gmail.com to get the link of this video5. Intersecting the x-axis at a distance of 3 units to the left of origin with slope –2.
Intersecting y-axis distance units above the origin7. Find equation of line passing Passing through the points (–1, 1) and (2, – 4).
8. Find the equation of line whose Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive x-axis is 30.
9. The vertices of ∆ PQR are P (2, 1), Q (–2, 3) and R (4, 5). Find equation of the median through the vertex R.
10. Find the equation of the line passing through (–3, 5) and perpendicular to the line through the points (2, 5) and (–3, 6).
11. A line perpendicular to the line segment joining the points (1, 0) and (2, 3) divides it in the ratio 1: n. Find the equation of the line.
12. Find the equation of a line that cuts off equal intercepts on the coordinate axes and passes through the point (2, 3).
13. Find equation of the line passing through the point (2, 2) and cutting off intercepts on the axes whose sum is 9.
14. Find equation of the line through the point (0, 2) making an angle 2π/3 with the positive x-axis. Also, find the equation of line parallel to it and crossing the y-axis at a distance of 2 units below the origin.
15. The perpendicular from the origin to a line meets it at the point (–2, 9), find the equation of the line.
16. The length L (in centimetrs) of a copper rod is a linear function of its Celsius temperature C. In an experiment, if L = 124.942 when C = 20 and L= 125.134 when C = 110, express L in terms of C.
17. The owner of a milk store finds that, he can sell 980 litres of milk each week at Rs 14/litre and 1220 litres of milk each week at Rs 16/litre. Assuming a linear relationship between selling price and demand, how many litres could he sell weekly at Rs 17/litre?
18. P (a, b) is the mid-point of a line segment between axes. Show that equation of the line is x/a + y/b = 2
19. Point R (h, k) divides a line segment between the axes in the ratio 1: 2. Find equation of the line.
20. By using the concept of equation of a line, prove that the three points (3, 0),(– 2, – 2) and (8, 2) are collinear.
1. Reduce the following equations into slope - intercept form and find their slopes and the y - intercepts. (i) x + 7y = 0, (ii) 6x + 3y – 5 = 0, (iii) y = 0.
2. Reduce the following equations into intercept form and find their intercepts on the axes. (i) 3x + 2y – 12 = 0, (ii) 4x – 3y = 6, (iii) 3y + 2 = 0.
3. Reduce the following equations into normal form. Find their perpendicular distances from the origin and angle between perpendicular and the positive x-axis. (i) x –3y + 8 = 0, (ii) y – 2 = 0, (iii) x – y = 4.
4. Find the distance of the point (–1, 1) from the line 12(x + 6) = 5(y – 2).
5. Find the points on the x-axis, whose distances from the line x/3 + y/4 =1 are 4 units.
6. Find the distance between parallel lines(i) 15x + 8y – 34 = 0 and 15x + 8y + 31 = 0 (ii) l (x + y) + p = 0 and l (x + y) – r = 0.
7. Find equation of the line parallel to the line 3x- 4y + 2 = 0 and passing through the point (–2, 3).
8. Find equation of the line perpendicular to the line x – 7y + 5 = 0 and having x intercept 3.
9. Find angles between the lines
10. The line through the points (h, 3) and (4, 1) intersects the line 7x -9y -19 = 0 at right angle. Find the value of h.
11. Prove that the line through the point (x 1 , y1 ) and parallel to the line Ax + By + C = 0 is A (x –x 1 ) + B (y – y1 ) = 0.
12. Two lines passing through the point (2, 3) intersects each other at an angle of 60 If slope of one line is 2, find equation of the other line.
Find the equation of the right bisector of the line segment joining the14. Find the coordinates of the foot of perpendicular from the point (–1, 3) to the line 3x – 4y – 16 = 0.
15. The perpendicular from the origin to the line y = mx + c meets it at the point (–1, 2). Find the values of m and c.
16. If p and q are the lengths of perpendiculars from the origin to the lines...
17. In the triangle ABC with vertices A (2, 3), B (4, –1) and C (1, 2), find the equation and length of altitude from the vertex A.
18. If p is the length of perpendicular from the origin to the line whose intercepts on ...
1. Find the values of k for which the line (k–3) x – (4 – k2) y + k2 –7k + 6 = 0 is (a) Parallel to the x-axis, (b) Parallel to the y-axis, (c) Passing through the origin.
2. Find the values of θ and p, if the equation x cos θ + y sinθ = p is the normal form ...
3. Find the equations of the lines, which cut-off intercepts on the axes whose sum and product are 1 and – 6, respectively.
4. What are the points on the y-axis whose distance from the line is ... 4 units.
5. Find perpendicular distance from the origin of the line joining the points (cosθ, sin θ) and (cos φ, sin φ).
6. Find the equation of the line parallel to y-axis and drawn through the point ofintersection of the lines x – 7y + 5 = 0 and 3x + y = 0.
7. Find the equation of a line drawn perpendicular to the line ... through the point, where it meets the y-axis.
8. Find the area of the triangle formed by the lines y – x = 0, x + y = 0 and x – k = 0.
9. Find the value of p so that the three lines 3x + y – 2 = 0, px + 2 y – 3 = 0 and 2x – y – 3 = 0 may intersect at one point.
10. If three lines whose equations are y = m1x + c1, y = m2x + c2 and y = m are concurrent, then show that ...
11. Find the equation of the lines through the point (3, 2) which make an angle of 45 with the line x – 2y = 3.
12. Find the equation of the line passing through the point of intersection of the lines 4x + 7y – 3 = 0 and 2x – 3y + 1 = 0 that has equal intercepts on the axes
13. Show that the equation of the line passing through the origin and making an angle θ with the line ...
14. In what ratio, the line joining (–1, 1) and (5, 7) is divided by the line x + y = 4?
15. Find the distance of the line 4x + 7y + 5 = 0 from the point (1, 2) along the line 2x – y = 0.
16. Find the direction in which a straight line must be drawn through the point (–1, 2) so that its point of intersection with the line x + y = 4 may be at a distance of 3 units from this point.
17. The hypotenuse of a right angled triangle has its ends at the points (1, 3) and (– 4, 1). Find the equation of the legs (perpendicular sides) of the triangle.
18. Find the image of the point (3, 8) with respect to the line x +3y = 7 assuming the line to be a plane mirror.
23. Prove that the product of the lengths of the perpendiculars drawn from the ...
24. A person standing at the junction (crossing) of two straight paths represented by the equations 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 wants to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find equation of the path that he should follow.
Copyright @ ncerthelp.com A free educational website for CBSE, ICSE and UP board.