NCERT Solutions Class 10 Mathematics Chapter 2: Polynomial Exercise 2.3

Concept Chapter 2 Class 10 Maths POLYNOMIALS Ncert Solutions

Degree of the polynomial :-

If p(x) is a polynomial in terms of x, the highest power of x in p(x) is called the degree of the polynomial p(x).
For example:
3x + 2 is a polynomial of x. Degree of expression is 1
4z^2 –z + 2 is a polynomial of z. Degree of expression is 2,
3x^3 – 2x – 2 is a polynomial of x. Degree of expression is 3

< style="color:#FF0000">

Type of polynomials

Linear polynomial :-

A polynomial of degree 1 is called a linear polynomial.

For example: 7x + 43

Quadratic polynomial :-

A polynomial of degree 2 is called a quadratic polynomial.

For example: x^2 + 3x + 7

Cubic polynomial :-

A polynomial of degree 3 is called a cubic polynomial

For example: x^3 + 3x Zeros of the polynomial :-

A real number t is called a zero of a polynomial if the value of f(t) = 0
For example
f(x) = x^2 – 6x +8
zeros of this equation are 2 and 4 because
f(2)= 2^2 -6*2 + 8 = 0
f(4)= 4^2 – 6*4 + 8 =0

Sum and product of root of quadratic equation :-
For a equation ax^2 + bx + c = 0 , if root are α and β ,

Roots for cubic equation :-
For a equation ax^3 + bx^2 + cx + d = 0

Division Algorithm:-

If p(x) and g(x) are any two polynomials with g(x) is not equal to 0, then we can find polynomials q(x) and r(x) such that
If r(x) = 0 or degree of r(x) < degree of g(x).
Dividend = Divisor × Quotient + Remainder
p(x) = g(x) × q(x) + r(x),

Exercise 2.1 Chapter 2 Class 10 Maths POLYNOMIALS Ncert Solutions

Question 1. The graphs of y = p(x) are given in Fig. 2.10 below, for some polynomials p(x). Find the number of zeroes of p(x), in each case.

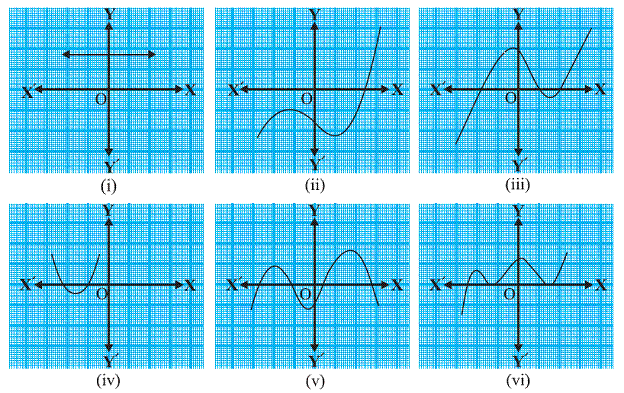
Answer
(i)the graph does not intersect the x axis so that there are no zero in this graph
(ii)the graph intersects the x axis at one places so that here are one zeros in this graph
(iii)the graph intersects the x axis at three places so that there are three zeros in this graph
(iv)the graph intersects the x axis at two places so there are two zeros in this graph
(v) the graph intersect the x axis at four places so there are four zeros in this graph
(vi) the graph intersects the x axis at three places so that there are three zeros in this graph

Exercise 2.2 Chapter 2 Class 10 Maths POLYNOMIALS Ncert Solutions

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(iii) 4u² + 8u

(iv) 4u² + 8u
Factorize the equation

Compare the equation with au² + bu + c = 0
We get
a = 4 ,b=-8 c= 0
To factorize the value we can take 4u common there
4u(u+2) = 0
First zero
4u = 0
U = 0
second zero
u+2 = 0
u = - 2

sum of zero 0 - 2 = - 2
product of zero 0 x ( - 2 ) = 0

Sum of zero -b/a = -(8/4) = -2
Product of zero c/a = 0/4 = 0

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(vi)3x² – x – 4

(vi) 3x² – x – 4
Factorize the equation
3x² – x – 4
Compare the equation with ax² + bx + c = 0
We get
a = 3 ,b=-1 c= -4
to factorize the value we have to find two value which
sum is equal to b =-1
product is a*c = 3*-4 = -12
3 and -4 are such number which
Sum is 3 – 4 = - 1
Product is 3 *- 4 = - 12
So we can write middle term -x = 3x – 4x
We get
3x² + 3x - 4x - 4 = 0
3x(x +1) -4(x + 1) = 0
(x + 1) (3x - 4) = 0
x + 1 = 0 , 3x - 4 = 0
Solve for first zero
x = - 1
solve for second zero
3x-4 = 0
3x = 4
x = 4/3

Sum of zeros -b/a = -(-1/3) = 1/3
Product of zero c/a = -4/3 = 4/3

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(v) t² – 15

(v) t² – 15
Factorize the equation
t² – 15 = 0
Add 15 both side we get
t² = 15
Take square root both side
t= ± √15
First zero is √15
second zerois - √15
Sum of zero √15 - √15 = 0
Product of zero √15 x -√15 = -15
Compare the equation with at² + bt +c = 0
We get
a = 1, b = 0, c = -15

Sum of zero -b/a = -(0/1) = 0
Product of zero c/a = -15/1 = -15

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(iii) 6x² – 3 – 7x

(iii) 6x² – 3 – 7x
Factorize the equation
6x² – 7x – 3
Compare the equation with ax² + bx + c = 0
We get
a = 6 ,b=-7 c= -3
To factorize the value we have to find two value which
sum is equal to b =-7
product is a x c = 6 x -3 = -18
2 and -9 are such number which
sum is 2 – 9 = - 7
product is 2 x - 9 = - 18
So we can write middle term -7x = 2x – 9x
We get

6x² + 2x - 9x - 3 = 0
2x(3x + 1) -3(3x + 1) = 0
(3x + 1) (2x - 3)= 0
3x + 1 = 0 , 2x - 3 = 0
Solve for first zero
3x = - 1
x = -1/3
Solve for second zero
2x-3 = 0
2x = 3
X = 3/2

Plug the values of a , b and c we get
Sum of zeros -b/a = -(-7/6) = 7/6
Product of zero c/a = -3/6 = -1/2

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.
(i) x² – 2x – 8

(i)

< style="padding-left:156px;">

Factorize the equation

Compare the equation with ax² + bx + c = 0
We get
a = 1 ,b=-2 c= -8
To factorize the value we have to find two value which
sum is equal to b =-2
and product is a x c = 1 x -8 = -8

2 and -4 are such number which

sum is 2-4 = - 2
product is 2*-4 = - 8

So we can write middle term -2 x = 2 x – 4 x
We get
x²+2x-4x-8=0
x (x + 2)-4(x + 2) = 0
(x+2) (x-4) = 0
First zero
x + 2 = 0
x = -2
Second zero
x-4 = 0
x = 4
sum of zero -2 + 4 = 2
product of zero 2 x -4 = -8

For a equation ax² + bx + c = 0 , if zeroare α and β ,

Plug the values of a , b and c we get
Sum of zeros -b/a = -(-2/1) = 2
Product of zeros c/a =-8/1 = -8

1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients.

(ii) 4s² – 4s + 1

Factorize the equation
Compare the equation with as² + bs + c = 0
We get
a = 4 , b = -4, c = 1
To factorize the value we have to find two value which
sum is equal to b = -4
product is a x c = 4
-2 and -2 are such number which
sum is (– 2)+( – 2) = - 4
product is (- 2 )* (- 2) = 4
So we can write middle term - 4s = -2s – 2s
We get
4s² - 2s - 2s + 1 = 0

2s(2s -1) -1(2s -1) = 0
(2s - 1) (2s - 1) = 0

Solve for first zero

2s - 1 =0
2s = 1
s = ½

Solve for second zero

2s - 1 =0
2s = 1
S = ½

sum of zeros ½ + ½ = 2/2 = 1
product of zeros ½ x ½ = 1/4

Sum of zero = -b/a = -(-4/4) = 1

Product of zero= c/a = 1/4 = 1/4

Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
(i)1/4 , -1 (ii) √2 , 1/3 (iii) 0, √5 (iv) 1,1 (v) -1/4 ,1/4 (vi) 4,1

(i)1/4, -1

Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(1/4)x -1 = 0
Multiply by 4 to remove denominator we get
4x² - x -4 = 0

(ii) √2 , 1/3
Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(√2)x + 1/3 = 0
Multiply by 3 to remove denominator we get
3x² - 3√2 x + 1 = 0

(iii) 0, √5
Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(0)x + √5 = 0
simplify it we get
x² + √5 = 0

(iv) 1,1
Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(1)x + 1 = 0
simplify it we get
x² - x + 1 = 0

(v) -1/4 ,1/4
Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(-1/4)x + 1/4 = 0
multiply by 4 we get
4x² + x + 1 = 0

(vi) 4,1
Now formula of quadratic equation is
x²-(Sum of root)x + (Product of root) = 0
Plug the value in formula we get
x² –(4)x + 1 = 0
x^2 –4x + 1 = 0

Exercise 2.3 Chapter 2 Class 10 Maths POLYNOMIALS Ncert Solutions

1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :

(i) p(x) = x³ – 3x² + 5x – 3, g(x) = x² – 2

So quotient = x-3 and remainder 7x - 9

(ii)p(x) = x⁴ – 3x² + 4x + 5, g(x) = x² + 1 – x

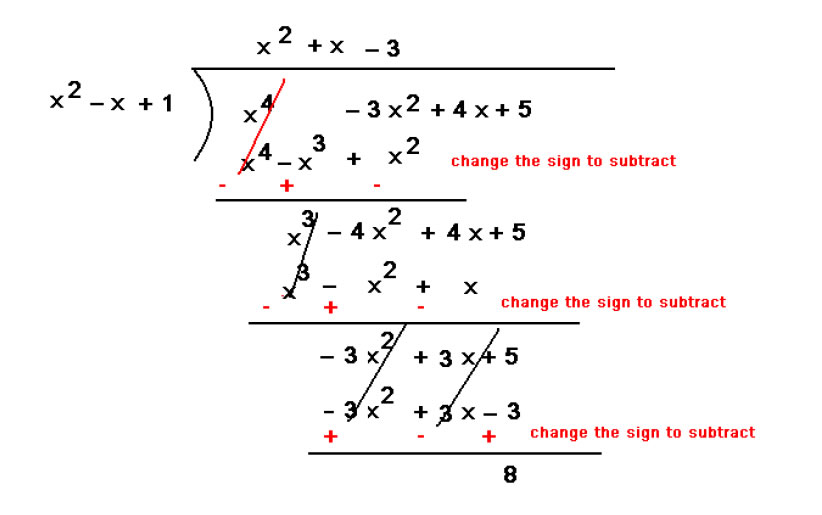
So quotient = x² + x-3 and remainder 8

(iii) p(x) = x⁴ – 5x + 6, g(x) = 2 – x²

Question 2. Check whether the first polynomial is a factor of the second polynomial by iding the second polynomial by the first polynomial:

(i)t² – 3, 2t⁴ + 3t³ – 2t² – 9t – 12

Remainder is 0 hence t² -3 is a factor of 2t⁴ + 3t³ – 2t² – 9t – 12

(ii)x² + 3x + 1, 3x⁴ + 5x³ – 7x² + 2x + 2

(iii)x³ – 3x + 1, x⁵ – 4x³ + x² + 3x + 1

Remainder is 2 so x³ – 3x + 1 is not a factor

Question 3. Obtain all other zeroes of 3x4 + 6x3 – 2x2 – 10x – 5, if two of its zeroes are √(5/3) and - √(5/3)

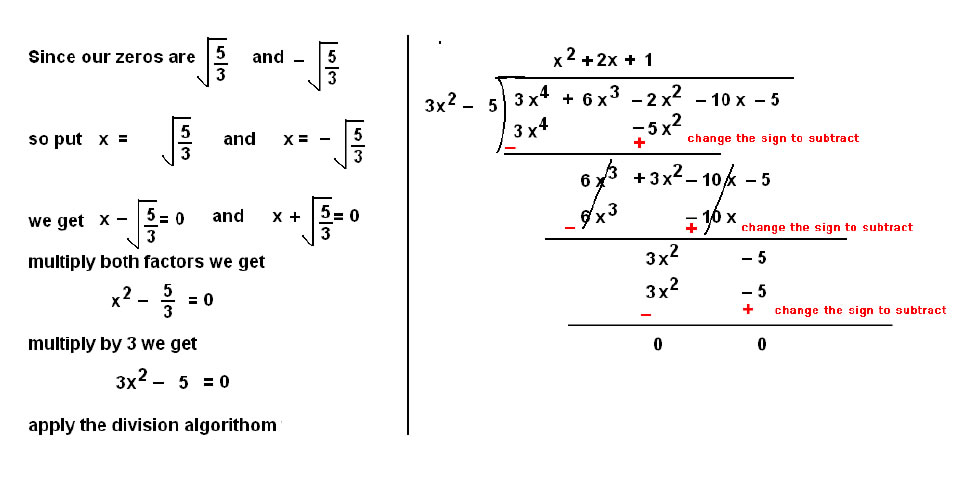
Quotient is x² + 2x + 1 = 0
Compare the equation with ax² + bx + c = 0
We get
a = 1 ,b = 2, c = 1
To factorize the value we have to find two value which
sum is equal to b = 2
product is a x c = 1 x 1 = 1
1 and 1 are such number which
sum is 1 + 1 = 2
product is 1 x 1 = 1
So we can write middle term 2x = x + x
We get
x² + x + x + 1 = 0
x (x +1) +1(x +1) = 0
( x + 1)( x + 1) = 0
x +1 = 0, x + 1= 0
x = -1 , x = - 1
so our zeroes are - 1 -1 , √(5/3) and - √(5/3)

Question 4. On iding x3 – 3x2 + x + 2 by a polynomial g(x), the quotient and remainder were x – 2 and –2x + 4, respectively. Find g(x).

According to ision algorithm
Dividen= Divisor × Quotient + Remainder
p(x) = g(x) × q(x) + r(x),
plug the value in formula we get
x³ – 3x² + x + 2 = g(x) *(x-2) - 2x + 4
Add 2x and subtract 4 both side we get

x³ – 3x² + x + 2 + 2x – 4 = g(x) *(x-2)

simplify and ide by x/2 we get

(x³ – 3x² + 3x– 2)/(x-2) = g(x)

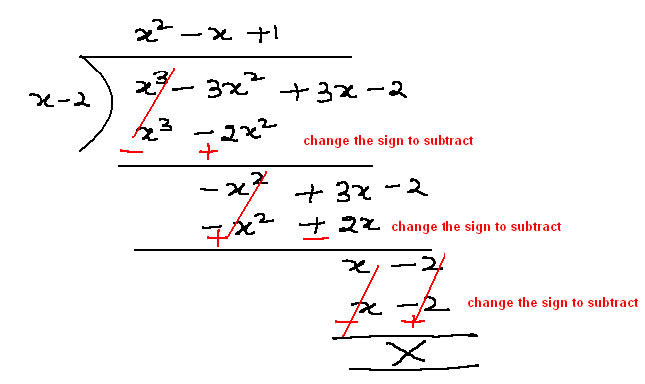
So we get g(x) = x^2 – x +1

Question5. Give examples of polynomials p(x), g(x), q(x) and r(x), which satisfy the ision algorithm

We can write many such examples
deg p(x) = deg q(x)
We can write many such examples
P(x) = x² , q(x) = x² g(x) = 1 R(x) = 0

(ii) deg q(x) = deg r(x)

Q(x) = x , R(x) = x , p(x) = x^3 + x g(x) = x²

(iii) deg r(x) = 0
Q(x) = 1 , R(x) = 1 , p(x) = x+1, g(x) = x

Ncert Solution for class 6 to 12 download in pdf