NCERT Solutions Class 10 Mathematics Chapter 1: Number System Exercise 1.4

Concept Chapter 1 Class 10 Maths REAL NUMBERS Ncert Solutions

Euclid’s Division Lemma For three positive integers a, b there exists a unique integer q and r such that a = bq + r and here value of r will always less then b
That means if we ide number a by b and q is our quotient and r is remainder then value of remainder will always less then deviser b .
For example 5 and 22
If we ide 22 by 5 we get 4 as quotient and 2 is remainder
So we can write it as 22= 5*4+ 2
And you can see that value of remainder is less then deviser

Composite number Every composite number can be expressed (factorized) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.

The Fundamental Theorem of Arithmetic If we ignore the order, any number which is more than 1, is either a prime number or can be written as unique product of prime number .
Or
Every composite number can be written in term of product of unique set of prime numbers ignoring their
For example
26 is a composite number and it can be written as 2*13 according to fundamental theorem you cannot get another set of value which product is 26.
So if we ignore the order of factors, prime factorization of all natural number is always unique.

Theorem of rational number: -

for any prime number p which is ides a^2 then it will ide a also.
For example: 5 ides 100 then it will ide root of 100( 10) also.

Theorem of terminator:-

for any rational number x which is written as p/q and if q can be written in form of 2^n*p^m and value of m and n are positive integer or equal to 0 then decimal expansion of x will terminate.

For example take x = 7/50
And 50 = 2*5*5 = 2^1*5^2
And powers 1 and 2 both are positive integer So value of x will terminate

Theorem of non-terminating repeating (recurring) :-

for any rational number x which is written as p/q and if q can’t be written in form of 2^n*p^m and value of m and n are positive integer or equal to 0 then decimal expansion of x will non-terminating repeating (recurring).
For example
X = 7/15
Here denominator 15 = 3*5
And it cannot be written in form of 2^n*5^m
x =0.4666……………
So x will non-terminating repeating (recurring) .

Exercise 1.1 Chapter 1 Class 10 Maths REAL NUMBERS Ncert Solutions

Question 1. Use Euclid’s ision algorithm to find the HCF of :
(i) 135 and 225 (ii) 196 and 38220 (iii) 867 and 255

Answer: (i)

Here 225 > 135 we always ide greater number with smaller one.
Divide 225 by 135 we get 1 quotient and 90 as remainder so that
225= 135*1 + 90
Divide 135 by 90 we get 1 quotient and 45 as remainder so that
135= 90*1 + 45
Divide 90 by 45 we get 2 quotient and no remainder so we can write it as
90 = 2*45+ 0
As there are no remainder so deviser 45 is our HCF

(ii)

38220>196 we always ide greater number with smaller one.
Divide 38220 by 196 then we get quotient 195 and no remainder so we can write it as
38220 = 196 * 195 + 0
As there is no remainder so deviser 196 is our HCF

(iii)
867>255we always ide greater number with smaller one.
ide 867 by 255 then we get quotient 3 and remainder is 102
so we can write it as
867 = 255 * 3 + 102
Divide 255 by 102 then we get quotient 2 and remainder is 51
So we can write it as
255 = 102 * 2 + 51
Divide 102 by 51 we get quotient 2 and no remainder
So we can write it as
102 = 51 * 2+ 0
As there is no remainder so deviser 51 is our answer

Question 2: Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.

Answer:

Let take a as any positive integer and b = 6.
Then using Euclid’s algorithm we geta = 6q + rhere r is remainder and value of q is more than or equal to 0 and r = 0, 1, 2, 3, 4, 5 because 0 <= r < band the value of b is 6
So total possible formswill6q+0 , 6q+1 , 6q+2,6q+3,6q+4,6q+5
6q+06 is isible by 2 so it is a even number
6q+16 is isible by 2 but 1 is not isible by 2 so it is a odd number
6q+26 is isible by 2 and 2 is also isible by 2 so it is a even number
6q+36 is isible by 2 but 3 is not isible by 2 so it is a odd number
6q+46 is isible by 2 and 4 is also isible by 2 it is a even number
6q+56 is isible by 2 but 5 is not isible by 2 so it is a odd number
So odd numbers will in form of 6q + 1, or 6q + 3, or 6q + 5

Question 3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?

Answer:

To get the maximum number column here we always find HCF and for minimum number we find LCM
So can use Euclid’s algorithm to find the HCF.
Here 616> 32 so always ide greater number with smaller one
When we ide 616 by 32 we get quotient 19 and remainder 8
So we can write it as
616 = 32 x 19 + 8
Now ide 32 by 8 we get quotient 4 and no remainder
So we can write it as
32 = 8 x 4 + 0
As there are no remainder so our HCF will 8

So that maximum number of columns in which they can march is 8.

4. Use Euclid’s ision lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Answer:

Let take a as any positive integer and b = 3.
Then using Euclid’s algorithm we geta = 3q + r here r is remainder and value of q is more than or equal to 0 and r = 0, 1, 2 because 0 < r < b and the value of b is 3 So our possible values will 3q+0 , 3q+1 and 3q+2

Now find the square of values
Use the formula (a+b)² = a² + 2ab +b² to open the square bracket
(3q)² = 9q² if we ide by 3 we get no remainder

we can write it as 3*(3q²) so it is in form of 3m here m = 3q²
(3q+1)² = (3q)² + 2*3q*1 + 1²
=9q² + 6q +1 now ide by 3 we get 1 remainder

so we can write it as 3(3q² + 2q) +1 so we can write it in form of 3m+1 and value of m is 3q² + 2q here
(3q+2)² = (3q)² + 2*3q*2 + 2²
=9q² + 12q +4 now ide by 3 we get 1 remainder

so we can write it as 3(3q² + 4q +1) +1 so we can write it in form of 3m +1 and value of m will 3q² + 4q +1
Square of any positive integer is either of the form 3m or 3m + 1 for some integer m.

Question 5. Use Euclid’s ision lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.

Answer:

According to Euclid’s Division Lemma
Let take a as any positive integer and b = 9.
Then using Euclid’s algorithm we get a = 9q + r here r is remainder and value of q is more than or equal to 0 and r = 0, 1, 2, 3, 4, 5 , 6 , 7 , 8, because 0 ≤r < b and the value of b is 9
Sp possible forms will 9q, 9q+1, 9q+2,9q+3,9q+4,9q+5,9q+6,9q+7 and 9q+8
to get the cube of these values use the formula
(a+b)³ = a³ + 3a²b+ 3ab² + b³
In this formula value of a is always 9q
So plug the value we get
(9q+b)³ = 729q³ + 243q²b + 27qb² + b³
Now ide by 9 we get quotient = 81q³ + 27q²b + 3qb² and remainder is b³
So we have to consider the value of b³
b = 0 we get 9m+0 = 9m
b = 1 then 1³ = 1 so we get 9m +1
b = 2 then 2³ = 8 so we get 9m + 8
b = 3 then 3³ = 27 and it is isible by 9 so we get 9m
b = 4 then 4³ =64 ide by 9 we get 1 as remainder so we get 9m +1
b=5 then 5³=125 ide by 9 we get 8 as remainder so we get 9m+8
b=6 then 6³=216 ide by 9 no remainder there so we get 9m
b=7 then 7³ = 343 ide by 9 we get 1 as remainder so we get 9m+1
b=8 then 8³ = 512 ide by 9 we get 8 as remainder so we get 9m+8
So all values are in form of 9m , 9m+1 or 9m+8

Exercise 1.2 Chapter 1 Class 10 Maths REAL NUMBERS Ncert Solutions

Question 1. Express each number as a product of its prime factors:
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429

Answer:

(i) 140 = 2 x 2 x 5 x 7 =2² x 5 x 7
(ii)156 =2 x 2 x 3 x 13 =2² x 3 x 13
(iii)3825 =3 x 3 x 5 x 5 x 17 =3² x 5² x 17
(iv)5005 =5 x 7 x 11 x 13 =5 x 7 x 11 x 13
(v)7429 =17 x 19 x 23 =17 x 19 x 23

Question 2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
26 and 91 (ii) 510 and 92 (iii) 336 and 54

Answer:

(i)

26 = 2 x 13
91 =7 x 13
HCF = 13
LCM =2 x 7 x 13 =182
Product of two value 26 x 91 = 2366
Product of HCF and LCM 13 x 182 = 2366
Hence, product of two numbers = product of HCF × LCM

(ii)

510 = 2 x 3 x 5 x 17
92 =2 x 2 x 23
HCF =2
LCM =2 x 2 x3 x 5 x 17 x 23 = 23460
Product of both values 510x92 = 46920
Product of HCF and LCM 2x23460 =46920
Hence, product of two numbers = product of HCF × LCM

(iii)

336 = 2 x 2 x 2 x 2 x 3 x 7
54 = 2 x 3 x 3 x 3
HCF = 2 x 3 = 6
LCM = 2 x 2 x 2 x 2 x 3 x 3 x 3 x 7 =3024
Product of number 336 x 54 =18144
Product of HCF and LCM 6 x 3024 = 18144
Hence, product of two numbers = product of HCF × LCM

Question 3. Find the LCM and HCF of the following integers by applying the prime factorization method.
(i) 12, 15 and 21 (ii) 17, 23 and 29 (iii) 8, 9 and 25

Answer:

(i)

12 = 2 x 2 x 3
15 =3 x 5
21 =3 x 7
HCF = 3
LCM = 2 x 2 x 3 x 5 x 7 = 420

(ii)

17 = 1 x 17
23 = 1 x 23
29 = 1 x 29
HCF = 1
LCM = 1 x 17 x 19 x 23 = 11339

(iii)

8 =1 x 2 x 2 x 2
9 =1 x 3 x 3
25 =1 x 5 x 5
HCF =1
LCM = 1 x 2 x 2 x 2 x 3 x 3 x 5 x 5 = 1800

Question 4. Given that HCF (306, 657) = 9, find LCM (306, 657).

Answer:

We have the formula that
Product of LCM and HCF = product of number
LCM x 9 = 306 x 657
Divide both side by 9 we get
LCM = (306 x 657)/ 9 = 22338

Question 5. Check whether 6n can end with the digit 0 for any natural number n.

Answer:

If any digit has last digit 10 that means It is isible by 10 And the factors of
10 = 2x5 So value 6n should be isible by 2 and 5 both 6n is isible by 2 but not isible by 5 So it can not end with 0.

Question 6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.

Answer:

7 × 11 × 13 + 13
Take 13 common there we get
13 (7 x 11 +1 )
13(77 + 1 )
13 (78)
It is product of two numbers and both numbers are more than 1 so it is a composite number

7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
Take 5 common there we get
5(7 x 6 x 4 x 3 x 2 x 1 +1)
5(1008 +1)
5(1009)
It is product of two numbers and both numbers are more than 1 so it is a composite number

Question 7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?

Answer:

They will be meet again after LCM of both values at the starting point.
To get the LCM we have to factorize the number.
18 = 2 × 3 × 3
12 = 2 × 2 × 3
LCM = 2 × 2 × 3 × 3 = 36
Therefore, they will meet together at the starting point after 36 minutes.

Exercise 1.3 Chapter 1 Class 10 Maths REAL NUMBERS Ncert Solutions

Question 1. Prove that √5 is irrational.

Answer:

Let take √5 as rational number
If a and b are two co prime number and b is not equal to 0.
We can write √5 = a/b
Multiply by b both side we get
b√5 = a
To remove root, Squaring on both sides, we get
5b² = a² ……………(1)
Therefore, 5 ides a² and according to theorem of rational number, for any prime number p which is ides a² then it will ide a also.
That means 5 will ide a. So we can write
a = 5c
and plug the value of a in equation (1) we get
5b² = (5c)²
5b² = 25c²
Divide by 25 we get
b²/5 = c²
again using same theorem we get that b will ide by 5
and we have already get that a is ide by 5
but a and b are co prime number. so it is contradicting .
Hence √5 is a non rational number

Question 2. Prove that 3 + 2√5 is irrational.

Answer:
Let take that 3 + 2√5 is a rational number.
So we can write this number as
3 + 2√5 = a/b
Here a and b are two co prime number and b is not equal to 0
Subtract 3 both sides we get
2√5 = a/b – 3
2√5 = (a-3b)/b
Now ide by 2 we get
√5 = (a-3b)/2b
Here a and b are integer so (a-3b)/2b is a rational number so √5 should be a rational number But √5 is a irrational number so it contradict the fact
Hence result is 3 + 2√5 is a irrational number

Question 3. Prove that the following are irrationals:
(i) 1/√2 (ii) 7√5 (iii) 6 + √2

Answer:
(i) Let take that 1/√2 is a rational number.
So we can write this number as
1/√2 = a/b
Here a and b are two co prime number and b is not equal to 0
Multiply by √2 both sides we get
1 = (a√2)/b
Now multiply by b
b = a√2
ide by a we get
b/a = √2
Here a and b are integer so b/a is a rational number so √2 should be a rational number But √2 is a irrational number so it is contradict
Hence result is 1/√2 is a irrational number

(ii) Let take that 7√5 is a rational number.
So we can write this number as
7√5 = a/b
Here a and b are two co prime number and b is not equal to 0
Divide by 7 we get
√5) =a/(7b)
Here a and b are integer so a/7b is a rational number so √5 should be a rational number but √5 is a irrational number so it is contradict
Hence result is 7√5 is a irrational number.

(iii) Let take that 6 + √2 is a rational number.
So we can write this number as
6 + √2 = a/b
Here a and b are two co prime number and b is not equal to 0
Subtract 6 both side we get
√2 = a/b – 6
√2 = (a-6b)/b
Here a and b are integer so (a-6b)/b is a rational number so √2 should be a rational number But √2 is a irrational number so it is contradict
Hence result is 6 + √2 is a irrational number

Exercise 1.4 Chapter 1 Class 10 Maths REAL NUMBERS Ncert Solutions

Question 1. Without actually performing the long ision, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i)13/3125 (ii)17/8 (iii)64/455
(iv)15/1600
(v)29/343
(vi)23/2³*5²
(vii)129/2²* 5⁷* 7⁵
(viii)6/15
(ix)35/50
(x)77/210

Answer:

(i) 13/3125
Factorize the denominator we get
3125 =5 x 5 x 5 x 5 x 5 = 5⁵
So denominator is in form of 5^m so 13/3125 is terminating .
(ii) 17/8
Factorize the denominator we get
8 =2 x 2 x 2 = 2³
So denominator is in form of 2ⁿ so 17/8 is terminating .
(iii) 64/455
Factorize the denominator we get
455 =5 x 7 x 13
There are 7 and 13 also in denominator so denominator is not in form of 2ⁿ*5^m . hence 64/455 is not terminating.
(iv) 15/1600
Factorize the denominator we get
1600 =2 x 2 x 2 x2 x 2 x 2 x 5 x 5 = 2⁶ x 5²
so denominator is in form of 2ⁿ x 5^m
Hence 15/1600 is terminating.
(v) 29/343
Factorize the denominator we get
343 = 7 x 7 x 7 = 7³
There are 7 also in denominator so denominator is not in form of 2ⁿ x 5^m
Hence it is none - terminating.
(vi) 23/(2³ x 5²)
Denominator is in form of 2ⁿ x 5^m
Hence it is terminating.
(vii) 129/(2² x 5⁷ x 7⁵ )
Denominator has 7 in denominator so denominator is not in form of 2ⁿ x 5ⁿ
Hence it is none terminating.
(viii) 6/15
ide nominator and denominator both by 3 we get 2/5
Denominator is in form of 5^m so it is terminating.

(ix) 35/50 ide denominator and nominator both by 5 we get 7/10
Factorize the denominator we get
10=2 x 5
So denominator is in form of 2ⁿ x5^m so it is terminating
(x) 77/210.
simplify it by iding nominator and denominator both by 7 we get 11/30
Factorize the denominator we get
30=2 x 3 x 5
Denominator has 3 also in denominator so denominator is not in form of 2ⁿ x 5ⁿ
Hence it is none terminating.

Question 2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.

(i)13/3125 = 0.009375

(ii)17/8

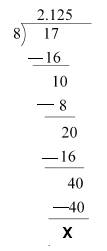
(iii)64/455 none- terminating

(iv)15/1600

(v)29/343 it is none – terminating

(vi)23/2³*5² = 23/200

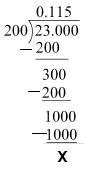
(vii)129/2²* 5⁷*7⁵ it is none terminating

(viii) 6/15 = 2/5 = 0.4

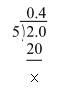
(ix)35/50

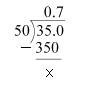
(x)77/210 it is none terminating

Question 3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form p , q you say about the prime factors of q?

Answer:

(i) 43.123456789
it has certain number of digits so they can be represented in form of p/q . Hence they are rational number
As they have certain number of digit and the number which has certain number of digits is always terminating number and for terminating number denominator has prime factor 2 and 5 only .

(ii) 0.120120012000120000. . .
In this problem repetitions number are not same so it is not a irrational number
so prime factor of denominator Q will has a value which is not equal to 2 or 5. And irrational number is always none terminating
(iii) 43.123456789
In this number 0.123456789 repeating again and again so it is a rational number and it is none terminating so that the prime factor has a value which is not equal to 2 or 5

Ncert Solution for class 6 to 12 download in pdf