CBSE Class 10 Maths Question Paper 2017 2018 2019 2020 Solved All Sets

Class 10 Subject Maths Paper Set 1 with Solutions

---

Question 1: (Marks 1)

HCF of 144 and 198 is

(a) 9

(b) 18

(c) 6

(d) 12

---

Answer :

(b) 18

---

Question 2: (Marks 1)

The median and mode respectively of a frequency distribution are 26 and 29. Then its mean is

(a) 27.5

(b) 24.5

(c) 28.4

(d) 25.8

---

Answer :

(b) 24.5

---

Question 3: (Marks 1)

In Fig. 1, on a circle of radius 7 cm, tangent PT is drawn from a point P such that PT = 24 cm. If 0 is the centre of the circle, then the length of PR is

(a) 30 cm

(b) 28 cm

(c) 32 cm

(d) 25 cm

---

Answer :

(c) 32 cm

---

Question 4: (Marks 1)

225 can be expressed as

(a) 5 × 3²

(b) 5² × 3

(c) 5² × 3²

(d) 5³ × 3

---

Answer :

(d) 5² × 3²

---

Question 5: (Marks 1)

---

Answer :

---

Question 6: (Marks 1)

---

Answer :

---

Question 7: (Marks 1)

Answer :

(b) a rational number

---

Question 8: (Marks 1)

The graph of a polynomial is shown in Fig. 2, then the number of its zeroes is

(a) 3

(b) 1

(c) 2

(d) 4

---

Answer :

(a) 3

---

Question 9: (Marks 1)

Distance of point P(3, 4) from x-axis is

(a) 3 units

(b) 4 units

(c) 5 units

(d) 1 unit

---

Answer :

(b) 4 units

---

Question 10: (Marks 1)

If the distance between the points A(4, p) and B(1, 0) is 5 units, then the value(s) of p is (are)

(a) 4 only

(b) –4 only

(c) ±4

(d) 0

---

Answer :

(c) ±4

---

Question 11: (Marks 1)

If the point C(k, 4) divides the line segment joining two points A(2, 6) and B(5, 1) in ratio 2 : 3, the value of k is _______.

OR

If points A(&nndash;3, 12), B(7, 6) and C(x, 9) are collinear, then the value of x is_______. Sol. 2

---

Answer :

OR

2

---

Question 12: (Marks 1)

If the equations kx – 2y = 3 and 3x + y = 5 represent two intersecting lines at unique point, then the value of k is _______.

OR

If quadratic equation 3x – 4x + k = 0 has equal roots, then the value of k is _______.

---

Answer :

. ≠ –6

OR

---

Question 13: (Marks 1)

The value of (sin 20° cos 70° + sin 70° cos 20°) is _______.

---

Answer :

1

---

Question 14: (Marks 1)

Answer :

45°

---

Question 15: (Marks 1)

The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of the first triangle is 9 cm, then the corresponding side of second triangle is _______.

---

Answer :

---

Question 16: (Marks 1)

---

Answer :

---

Question 17: (Marks 1)

The areas of two circles are in the ratio 9 : 4, then what is the ratio of their circumferences?

---

Answer :

---

Question 18: (Marks 1)

If a pair of dice is thrown once, then what is the probability of getting a sum of 8?

---

Answer :

Favourable outcomes are (3, 5); (4, 4); (5, 3); (2, 6); (6, 2) i.e., 5

---

Question 19: (Marks 1)

In Fig. 3, in ΔABC, DE || BC such that AD = 2.4 cm, AB = 3.2 cm and AC = 8 cm, then what is the length of AE?

---

Answer :

---

Question 20: (Marks 1)

The nth term of an AP is (7 – 4n), then what is its common difference?

---

Answer :

T1 = 3, T2 = –1

d = –4

---

Question 21: (Marks 2)

A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball at random from the bag is three times that of a red ball, find the number of blue balls in the bag.

---

Answer :

---

Question 22: (Marks 2)

OR

---

Answer :

OR

---

Question 23: (Marks 2)

Two different dice are thrown together, find the probability that the sum of the numbers appeared is less than 5.

OR

Find the probability that 5 Sundays occur in the month of November of a randomly selected year.

---

Answer :

---

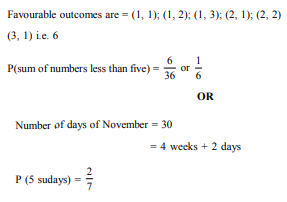
Question 24: (Marks 2)

In Fig. 4, a circle touches all the four sides of a quadrilateral ABCD. If AB = 6 cm, BC = 9 cm and CD = 8 cm, then the find length of AD

---

Answer :

The sides of quadrilateral touches a circle

AB + DC = BC + AD

6 + 8 = 9 + AD ⇒ AD = 5 cm

---

Question 25: (Marks 2)

The perimeter of a sector of a circle with radius 6.5 cm is 31 cm, then find the area of the sector.

---

Answer :

---

Question 26: (Marks 2)

Divide the polynomial (4x² + 4x + 5) by (2x + 1) and write the quotient and the remainder.

---

Answer :

---

Question 27: (Marks 3)

I f α and β are the zeroes of the polynomial f(x) = x² – 4x - 5 then find the value of α² + β² .

---

Answer :

---

Question 28: (Marks 3)

Draw a circle of radius 4 cm. From a point 7 cm away from the centre of circle. Construct a pair of tangents to the circle.

OR

Draw a line segment of 6 cm and divide it in the ratio 3 : 2.

---

Answer :

Constructing the circle of given radius

Constructing the tangents

OR

Drawing line segment of length 6 cm.

Dividing it in the ratio 3 : 2.

---

Question 29: (Marks 3)

A solid metallic cuboid of dimension 24 cm × 11 cm × 7 cm is melted and recast into solid cones of base radius 3.5 cm and height 6 cm. Find the number of cones so formed

---

Answer :

---

Question 30: (Marks 3)

Prove that (1 + tan A – sec A) × (1 + tan A + sec A) = 2 tan A

OR

---

Answer :

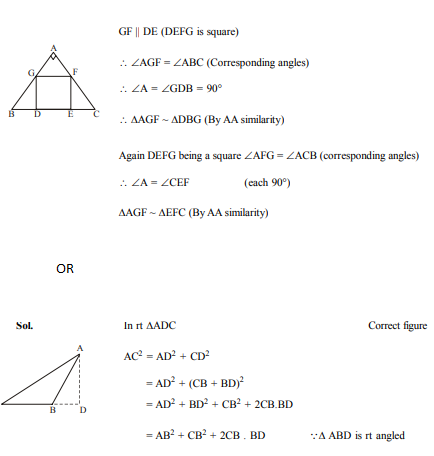
L.H.S. = (1 + tan A)² – sec² A

= 1 tan² A + 2 tan A – sec² A

= sec² A + 2tan A – sec² A

= 2 tan A = R.H.S.

OR

---

Question 31: (Marks 3)

OR

An army contingent of 612 members is to march behind an army band of 48 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?

---

Answer :

OR

612 = 2² × 3² × 17

48 = 2⁴ × 3

HCF (612, 48) = 2² × 3

= 12

Number of column = 12

---

Question 32: (Marks 3)

Prove that, in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

---

Answer :

Correct figure, given, To prove and construction.

Correct Proof

---

Question 33: (Marks 3)

---

Answer :

---

Question 34: (Marks 3)

Solve graphically: 2x + 3y = 2, x – 2y = 8

---

Answer :

Correct graph of 2x + 3y = 2

Correct graph of x – 2y = 8

Point of intersection = (4, –2)

or x = 4, y = – 2

---

Question 35: (Marks 4)

A two digit number is such that the product of its digits is 14. If 45 is added to the number; the digits interchange their places. Find the number.

---

Answer :

Let unit digit = x

Tens digit = y

∴ Number = 10y + x

10y + x + 45 = 10x + y

⇒ x – y = 5 ...(i)

and xy = 14 ...(ii)

Solving (i) and (ii)

x = 7, y = 2

∴ Number = 27

---

Question 36: (Marks 4)

If 4 times the 4th term of an AP is equal to 18 times the 18th term, then find the 22nd term.

OR

How many terms of the AP : 24, 21, 18, ... must be taken so that their sum is 78?

---

Answer :

Let first term be a and common difference = d

∴ 4(a + 3d) = 18(a + 17d)

⇒ a = –21d 1 22nd term = a + 21d

= –21d + 21d

= 0

OR

---

Question 37: (Marks 4)

The angle of elevation of the top of a building from the foot of a tower is 30°. The angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.

---

Answer :

---

Question 38: (Marks 4)

In Fig. 6, DEFG is a square in a triangle ABC right angled at A. Prove that

(i) ΔAGF ~ ΔDBG

(ii) ΔAGF ~ ΔEFC

OR

In an obtuse ΔABC (∠B is obtuse), AD is perpendicular to CB produced. Then prove that AC2 = AB2 + BC2 + 2BC × BD.

---

Answer :

---

Question 39: (Marks 4)

An open metal bucket is in the shape of a frustum of cone of height 21 cm with radii of its lower and upper ends are 10 cm and 20 cm respectively. Find the cost of milk which can completely fill the bucket at the rate of ` 40 per litre.

OR

A solid is in the shape of a cone surmounted on a hemisphere. The radius of each of them being 3.5 cm and the total height of the solid is 9.5 cm. Find the volume of the solid.

---

Answer :

---

Question 40: (Marks 4)

Find the mean of the following data:

---

Answer :

CBSE Class 10 Maths Question Paper 2017 2018 2019 2020 Solved all Sets

class 10 Maths sample paper 2020 solved, sample paper class 10 Maths, cbse class 10 Maths question paper 2018, sample paper class 10 Maths 2019, Maths question paper for class 10, cbse previous year question papers class 10 Maths, cbse sample paper for class 10 Maths, cbse class 10 Maths question paper 2019, class 10 Maths sample paper 2019 solved, cbse class 10th Maths question paper, 10th Maths question paper, sample paper class 10 Maths 2020, Maths sample paper class 12, cbse question paper for class 9 Maths, cbse Maths sample paper, cbse 10th class Maths

Ncert Solution for class 6 to 12 download in pdf