Maths Question Paper For Class 10 2018 2019 2020 CBSE Board NCERT Books

Class 10 Subject Maths Paper Set 2 with Solutions

---

Question 1: (Marks 1)

HCF of two numbers is 27 and their LCM is 162. If one of the number is 54, then the other number is

(a) 36

(b) 35

(c) 9

(d) 81

---

Answer :

(d) 81

---

Question 2: (Marks 1)

The cumulative frequency table is useful in determining

(a) Mean

(b) Median

(c) Mode

(d) All of these

---

Answer :

(b) Median

---

Question 3: (Marks 1)

In Fig. 1, O is the centre of circle. PQ is a chord and PT is tangent at P which makes an angle of 50° with PQ. ?POQ is

(a) 130°

(b) 90°

(c) 100°

(d) 75°

---

Answer :

(c) 100°

---

Question 4: (Marks 1)

(a) an integer

(b) a rational number

(c) an irrational number

(d) a whole number

---

Answer :

(c) an irrational no.

---

Question 5: (marks 1)

---

Answer :

---

Question 6: (Marks 1)

---

Answer :

3

---

Question 7: (Marks 1)

(a) 2

(b) 4

(c) 5

(d) 1

---

Answer :

(c) 5

---

Question 8: (Marks 1)

The maximum number of zeroes a cubic polynomial can have, is

(a) 1

(b) 4

(c) 2

(d) 3

---

Answer :

(d) 3

Question 9: (Marks 1)

The distance of the point (–12, 5) from the origin is

(a) 12

(b) 5

(c) 13

(d) 169

---

Answer :

(c) 13

---

Question 10: (Marks 1)

If the centre of a circle is (3, 5) and end points of a diameter are (4, 7) and (2, y), then the value of y is

(a) 3

(b) –3

(c) 7

(d) 4

---

Answer :

(a) 3

---

Question 11: (Marks 1)

The area of triangle formed with the origin and the points (4, 0) and (0, 6) is ________.

OR

The co-ordinate of the point dividing the line segment joining the points A(1, 3) and B(4, 6) in the ratio 2 : 1 is ________.

---

Answer :

12 sq units

OR

(3, 5)

---

Question 12: (Marks 1)

Value of the roots of the quadratic equation, x² – x – 6 = 0 are ________.

---

Answer :

3 and –2

---

Question 13: (Marks 1)

---

Answer :

---

Question 14: (Marks 1)

The value of (tan² 60° + sin² 45°) is ________.

---

Answer :

---

Question 15: (Marks 1)

The corresponding sides of two similar triangles are in the ratio 3 : 4, then the ratios of the area of triangles is _________.

---

Answer :

9 : 16

---

Question 16: (Marks 1)

Find the value of (cos 48° – sin 42°).

OR

Evaluate: (tan 23°) × (tan 67°)

---

Answer :

cos 48° – cos (90 – 42°)

cos 48° – cos 48° = 0

OR

tan (90 – 67°) × tan 67°

cot 67° × tan 67°

= 1

---

Question 17: (Marks 1)

---

Answer :

---

Question 18: (Marks 1)

A card is drawn at random from a well shuffled deck of 52 playing cards. What is the probability of getting a black king?

---

Answer :

---

Question 19: (Marks 1)

A ladder 25 m long just reaches the top of a building 24 m high from the ground. What is the distance of the foot of ladder from the base of the building?

---

Answer :

---

Question 20: (Marks 1)

If 3k – 2, 4k – 6 and k + 2 are three consecutive terms of A.P., then find the value of k.

---

Answer :

(4k – 6) – (3k – 2) = (k + 2) – (4k – 6)

⇒ k = 3

---

Question 21: (Marks 2)

In a lottery, there are 10 prizes and 25 blanks. What is the probability of getting a prize?

---

Answer :

---

Question 22: (Marks 2)

In a family of three children, find the probability of having at least two boys.

OR

Two dice are tossed simultaneously. Find the probability of getting

(i) an even number on both dice.

(ii) the sum of two numbers more than 9.

---

Answer :

---

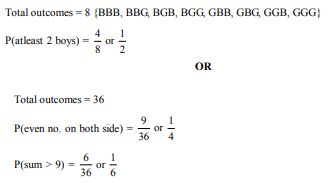
Question 23: (Marks 2)

Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of larger circle which touches the smaller circle.

---

Answer :

---

Question 24: (Marks 2)

---

Answer :

---

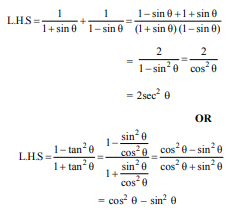
Question 25: (Marks 2)

The wheel of a motorcycle is of radius 35 cm. How many revolutions are required to travel a distance of 11 m?

---

Answer :

---

Question 26: (Marks 2)

Divide (2x² – x + 3) by (2 – x) and write the quotient and the remainder

---

Answer :

---

Question 27: (Marks 3)

---

Answer :

---

Question 28: (Marks 3)

Draw a line segment of length 7 cm and divide it in the ratio 2 : 3.

OR

Draw a circle of radius 4 cm and construct the pair of tangents to the circle from an external point, which is at a distance of 7 cm from its centre.

---

Answer :

Correct construction

OR

Correct construction

---

Question 29: (Marks 3)

The minute hand of a clock is 21 cm long. Calculate the area swept by it and the distance travelled by its tip in 20 minutes.

---

Answer :

---

Question 30: (Marks 3)

If x = 3 sin θ + 4 cos θ and y = 3 cos θ – 4 sin θ then prove that x² + y² = 25

OR

If sin θ + sin² θ = 1; then prove that cos² θ + cos⁴ θ = 1.

---

Answer :

x² = 9 sin² θ + 16 cos² θ + 24 sin θ cos θ

y² = 9 cos² θ + 16 sin² θ – 24 sin θ cos θ

x² + y² = 25

OR

sin θ = 1 – sin² θ = cos² θ

L.H.S = cos² θ + (cos² θ) ² = cos² θ + sin² θ

= 1 = R.H.S

---

Question 31: (Marks 3)

OR

Using Euclid’s algorithm, find the HCF of 272 and 1032.

---

Answer :

OR

1032 = 272 × 3 + 216

272 = 216 × 1 + 56

216 = 56 × 3 + 48

56 = 48 × 1 + 8

48 = 8 × 6 + 0 HCF(1032, 272) = 8

---

Question 32: (marks 3)

In a rectangle ABCD, P is any interior point. Then prove that PA² + PC² = PB² + PD² .

---

Answer :

---

Question 33: (Marks 3)

In a classroom, 4 friends are seated at the points A, B, C and D as shown in Fig. 3. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using distance formula, find which of them is correct.

---

Answer :

---

Question 34: (Marks 3)

Solve graphically:

2x – 3y + 13 = 0; 3x – 2y + 12 = 0

---

Answer :

Correct graph of 2x – 3y + 13 = 0, 3x – 2y + 12 = 0

Solution x = –2, y = 3

---

Question 35: (Marks 4)

The product of two consecutive positive integers is 306. Find the integers

---

Answer :

Let two consecutive integers x, x + 1

x(x + 1) = 306 ⇒ x2 + x – 306 = 0

⇒ (x + 18) (x – 17) = 0

⇒ x = –18, (Rejected), 17

∴ Two consecutive integers 17, 18

---

Question 36: (Marks 4)

The 17^th term of an A.P. is 5 more than twice its 8th term. If 11th term of A.P. is 43; then find its nth term.

OR

How many terms of A.P. 3, 5, 7, 9, ... must be taken to get the sum 120?

---

Answer :

a₁₇ = 2a₈ + 5 ⇒ a + 16d = 2(a + 7d) + 5

⇒ 2d – a = 15 ...(1)

a₁₁ = 43 ⇒ a + 10d = 43 ...(2)

Solving (1) & (2) a = 3 d = 4

a_n = 4n – 1

OR

---

Question 37: (Marks 4)

A person standing on the bank of a river observes that the angle of elevation of the top of a tree standing on opposite bank is 60°. When he moves 30 m away from the bank, he finds the angle of elevation to be 30°. Find the height of the tree and width of the river. [Take √3 = 1.732]

---

Answer :

---

Question 38: (Marks 4)

Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

OR

Prove that the length of tangents drawn from an external point to a circle are equal.

---

Answer :

Correct Fig., given, to prove, construction

Correct proof given, to prove, construction,

OR

Correct Fig., given, to prove, construction

Correct proof given, to prove, construction,

---

Question 39: (Marks 4)

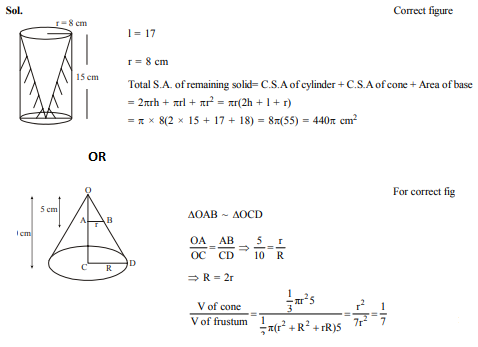
From a solid cylinder whose height is 15 cm and the diameter is 16 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of remaining solid. (Give your answer in terms of π).

OR

The height of a cone is 10 cm. The cone is divided into two parts using a plane parallel to its base at the middle of its height. Find the ratio of the volumes of the two parts.

---

Answer :

---

Question 40: (Marks 4)

The mode of the following frequency distribution is 36. Find the missing frequency (f).

---

Answer :

Maths Question Paper For Class 10 2018 2019 2020 CBSE Board NCERT Books

class 10 Maths sample paper 2020 solved, sample paper class 10 Maths, cbse class 10 Maths question paper 2018, sample paper class 10 Maths 2019, Maths question paper for class 10, cbse previous year question papers class 10 Maths, cbse sample paper for class 10 Maths, cbse class 10 Maths question paper 2019, class 10 Maths sample paper 2019 solved, cbse class 10th Maths question paper, 10th Maths question paper, sample paper class 10 Maths 2020, Maths sample paper class 12, cbse question paper for class 9 Maths, cbse Maths sample paper, cbse 10th class Maths

Ncert Solution for class 6 to 12 download in pdf