CBSE Previous Year Question Papers Class 10 Maths Chapter wise 2018 19 20

Here we are providing CBSE Previous Year Question Papers Class 6 to 12 solved with soutions CBSE Previous Year Question Papers Class 10 Maths Chapter wise 2018 19 20 class 10 Maths sample paper 2020 solved, sample paper class 10 Maths, cbse class 10 Maths question paper 2018, sample paper class 10 Maths 2019, Maths question paper for class 10, cbse previous year question papers class 10 Maths, cbse sample paper f Practice of previous year question papers and sample papers protects each and every student to score bad marks in exams.If any student of CBSE Board continuously practices last year question paper student will easily score high marks in tests. Fortunately earlier year question papers can assist the understudies with scoring great in the tests. Unraveling previous year question paper class 10 Maths is significant for understudies who will show up for Class 10 Board tests.

Class 10 Subject Maths Paper Set 3 with Solutions

SECTION A

Question numbers 1 to 10 are multiple choice questions of 1 mark each. Select the correct choice.

Question 1: (Marks 1)

What is the largest number that divides 245 and 1029, leaving remainder 5 in each?

(a) 15

(b) 16

(d) 5

Answer :

(b) 16

Question 2: (Marks 1)

$Consider the following distribution:$

Answer :

(b) 25

Question 3: (Marks 1)

$If the two tangents inclined at an angle of 60º are drawn to a circle of radius 3 cm, then the$

Answer :

$If the two tangents inclined at an angle of 60º are drawn to a circle of radius 3 cm, then the$

Question 4: (Marks 1)

$The simplest form of$

Answer :

$The simplest form of$

Question 5: (Marks 1)

$One card is drawn at random from a well – shuffled deck of 52 cards. What is the probability$

Answer :

$One card is drawn at random from a well – shuffled deck of 52 cards. What is the probability$

Question 6: (Marks 1)

$If one zero of the quadratic polynomial$

Answer :

$If one zero of the quadratic polynomial$

Question 7: (Marks 1)

$Which of the following rational numbers is expressible as a terminating decimal?$

Answer :

$Which of the following rational numbers is expressible as a terminating decimal?$

Question 8: (Marks 1)

$If a and ß are the zeros of (2x2$

Answer :

$If a and ß are the zeros of (2x2$

Question 9: (Marks 1)

$The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is$

Answer :

(d) 12

Question 10: (Marks 1)

If P(–1, 1) is the midpoint of the line segment joining A(–3, b) and B(1, b + 4), then b is equal to

(a) 1

(b) –1

(d) 0

Answer :

(b) –1

In Question numbers 11 to 15, fill in the blanks:

Question 11: (Marks 1)

Distance between (a, –b) and (a, b) is ________.

Answer :

2b units

Question 12: (Marks 1)

The value of k for which system of equations x + 2y = 3 and 5x + ky = 7 has no solution is ________.

Answer :

k = 10

Question 13: (Marks 1)

The value of (cos² 45º + cot² 45º) is ________.

Answer :

$The value of$

Question 14: (Marks 1)

The value of (tan 27º – cot 63º) is ________.

Answer :

Question 15: (Marks 1)

If ratio of the corresponding sides of two similar triangles is 2:3, then ratio of their perimeters is _________.

Answer :

2 : 3

Answer the following questions, Question numbers 16 to 20

Question 16: (Marks 1)

$then find the value of cot ?.$

Answer :

$then find the value of cot ?.$

Question 17: (Marks 1)

The perimeter of a sector of a circle of radius 14 cm is 68 cm. Find the area of the sector.

The circumference of a circle is 39.6 cm. Find its area.

Answer :

l = 68 – 28 = 40 cm

A = 280 cm²

$The circumference of a circle is 39.6 cm. Find its area.$

Question 18: (Marks 1)

A letter of English alphabet is chosen at random. Determine the probability that chosen letter is a consonant.

Answer :

No. of consonents = 21

$A letter of English alphabet is chosen at random. Determine the probability that chosen letter$

Question 19: (Marks 1)

In Fig. 1, D and E are points on sides AB and AC respectively of a ΔABC such that DE || BC. If AD = 3.6 cm, AB = 10 cm and AE =4.5 cm, find EC and AC.

$In Fig. 1, D and E are points on sides AB and AC respectively of a ?ABC such that DE || BC.$

Answer :

. EC = 8 cm

AC = 12.5 cm

Question 20: (marks 1)

If 3y – 1, 3y + 5 and 5y + 1 are three consecutive terms of an A.P., then find the value of y

Answer :

2(3y + 5) = 3y – 1 + 5y + 1

y = 5

SECTION B

Question numbers 21 to 26 carry 2 marks each.

Question 21: (Marks 2)

A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find the probability that the drawn ball is

(i) red or white

(ii) not a white ball

Answer :

$A bag contains 5 red, 8 white and 7 black balls. A ball is drawn at random from the bag. Find$

Question 22: (Marks 2)

Two dice are thrown at the same time. Find the probability of getting different numbers on the two dice.

Two dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is more than 9.

Answer :

$Two dice are thrown at the same time. Find the probability of getting different numbers on the$

Question 23: (Marks 2)

In Fig. 2, a circle is inscribed in a ΔABC, touching BC, CA and AB at P, Q and R respectively. If AB = 10 cm, AQ = 7 cm and CQ = 5 cm then find the length of BC.

$Fig. 2, a circle is inscribed in a ?ABC, touching BC, CA and AB at P, Q and R respectively$

Answer :

AQ = AR = 7 cm

BR = AB – AR = 10 – 7 = 3 cm

BC = BP + PC = BR + CQ

= 3 + 5 = 8 cm

Question 24: (Marks 2)

$Prove that:$

Answer :

$Prove that:$

Question 25: (Marks 2)

Three cubes each of volume 216 cm³ are joined end to end to form a cuboid. Find the total surface area of resulting cuboid.

Answer :

a³ = 216 cm³

a = 6 cm

TSA of cuboid = 5a² + 4a² + 5a²

= 14a²

= 504 cm²

Question 26: (Marks 2)

Find the values of p for which the quadratic equation x² – 2px + 1 = 0 has no real roots.

Answer :

For no real roots

D < 0 (–2p)2 – 4 × 1 × 1 < 0

p2 – 1 < 0

–1 < p < 1

SECTION C

Question numbers 27 to 34 carry 3 marks each.

Question 27: (Marks 3)

If 1 and –2 are the zeroes of the polynomial (x³ – 4x² – 7x + 10), find its third zero.

Answer :

$If 1 and –2 are the zeroes of the polynomial$

Question 28: (Marks 3)

Draw a circle of radius 3 cm. From a point 7 cm away from its centre, construct a pair of tangents to the circle.

Draw a line segment of 8 cm and divide it in the ratio 3 : 4.

Answer :

Drawing a circle of radius 3 cm, marking

Centre 0 and taking a point P such that

OP = 7 cm

Constructing two tangents

Drawing a line segment of 8 cm

Dividing it in the ratio 3 : 4

Question 29: (Marks 3)

$A wire when bent in the form of an equilateral triangle encloses an area of$

Answer :

$A wire when bent in the form of an equilateral triangle encloses an area of$

Question 30: (Marks 3)

$Prove that$

Prove that (sin θ + cosec θ)² + (cos θ + sec θ)² = 7 + tan² θ + cot² θ.

Answer :

$Prove that$

(sin θ + cosec θ)² + (cos θ + sec θ)²

= sin² θ + cosec² θ + 2 + cos² θ + sec² θ + 2

= sin² θ + 1 + cot² θ + 2 + cos² θ + 1 + tan² θ + 2

= 7 + tan² θ + cot² θ

Question 31: (Marks 3)

$If 2 is given as an irrational number, then prove that$

Find HCF of 44, 96 and 404 by prime factorization method. Hence find their LCM.

Answer :

$Find HCF of 44, 96 and 404 by prime factorization method. Hence find their LCM.$

Question 32: (Marks 3)

Prove that the parallelogram circumscribing a circle is a rhombus

Answer :

$Prove that the parallelogram circumscribing a circle is a rhombus.$

Question 33: (Marks 3)

In Fig. 3, arrangement of desks in a classroom is shown. Ashima, Bharti and Asha are seated at A, B and C respectively. Answer the following:

(i) Find whether the girls are sitting in a line.

(ii) If A, B and C are collinear, find the ratio in which point B divides the line segment joining A and C.

$In Fig. 3, arrangement of desks in a classroom is shown. Ashima, Bharti and Asha are seated$

Answer :

$In Fig. 3, arrangement of desks in a classroom is shown. Ashima, Bharti and Asha are seated$

Question 34: (Marks 3)

A number consists of two digits whose sum is 10. If 18 is subtracted from the number, its digit are reversed. Find the number.

Answer :

Let two digit number = 10x + y

x + y = 10 ...(i)

10x + y – 18 = 10y + x

⇒ x – y = 2 ...(ii)

On solving (i) & (ii) x = 6, y = 4

∴ Required number = 64

SECTION D

Question Nos. 35 to 40 carry 4 marks each.

Question 35: (Marks 4)

Some students planned a picnic. The total budget for food was ` 2,000 but 5 students failed to attend the picnic and thus the cost for food for each member increased by ` 20. How many students attended the picnic and how much did each student pay for the food?

Answer :

$Some students planned a picnic. The total budget for food wa$

Question 36: (Marks 4)

The sum of first 6 terms of an A.P. is 42. The ratio of its 10th term to 30^th term is 1:3. Find the first and the 13th term of the A.P.

Find the sum of all odd numbers between 100 and 300

Answer :

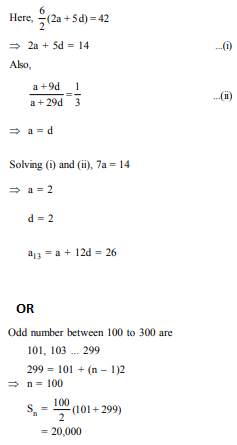
$The sum of first 6 terms of an A.P. is 42. The ratio of its 10th term to$

Question 37: (Marks 4)

$From the top of a 7 m high building, the angle of elevation of the top of a cable tower is$

Answer :

$From the top of a 7 m high building, the angle of elevation$

Question 38: (Marks 4)

In a right triangle, prove that the square of the hypotenuse is equal to sum of squares of the other two sides.

Prove that the tangents drawn from an external point to a circle are equal in length.

Answer :

For correct given, to prove, construction and figure

For correct proof

For correct given, to prove, construction and figure

For correct proof

Question 39: (Marks 4)

A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm, such that the diameter of the hemisphere is equal to edge of the cube. Determine the volume of the remaining block.

A solid metallic cylinder of diameter 12 cm and height 15 cm is melted and recast into 12 toys in the shape of a right circular cone mounted on a hemisphere of same radius. Find the radius of the hemisphere and total height of the toy, if the height of the cone is 3 times the radius.

Answer :

$A hemispherical depression is cut out from one face of a cubical wooden block of edge 21 cm,$