Linear Method of Solving Linear Equation of Two Variables All I Notes Chapter 3 Pair of Linear Equations in Two

Linear equations: Two linear equations in the same two variables are called a pair of linear equations in two variables. The most general form of a pair of linear equations is

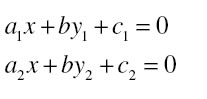
Where a1, a2, b1, b2, c1, c2  are real numbers, such that    

Method of solving linear equation of two variables
A pair of linear equations in two variables can be represented, and solved, by the:
(i)graphical method             (ii) algebraic method

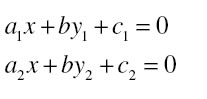
All in one table for this chapter
If a pair of linear equations are
Then

Conclusion from the  table

Graphical Method :
The graph of a pair of linear equations in two variables is represented by two lines.
(i) If the lines intersect at a point, then that point gives the unique solution of the two equations. In this case, the pair of equations is consistent.
(ii) If the lines coincide, then there are infinitely many solutions — each point on the line being a solution. In this case, the pair of equations is dependent (consistent).
(iii) If the lines are parallel, then the pair of equations has no solution. In this case, the pair of equations is inconsistent.

Algebraic Methods : We have discussed the following methods for finding the solution(s) of a pair of linear equations :
(i) Substitution Method
(ii) Elimination Method
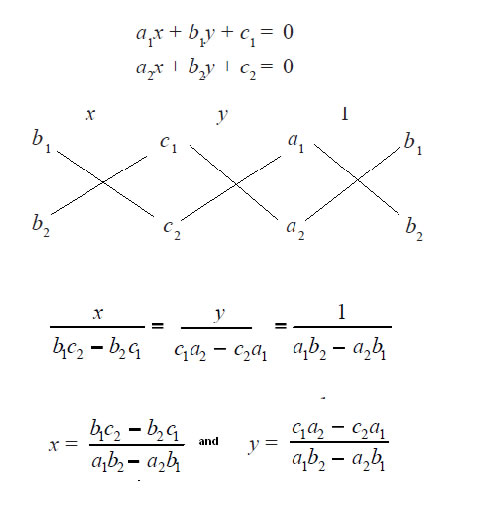
(iii) Cross-multiplication Method
Formula of cross multiplication is